Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 0.1 (exercícios de compreensão) - Ex. 3

A figura dada mostra o gráfico completo de   y   =   f ( x ) .

  1. O domínio de f é __________.
  2. A imagem de f é __________.
  3. f ( - 3 ) = __________.
  4. f 1 2 = __________.
  5. As soluções de f x = - 3 2 são x = __________ e x = __________.

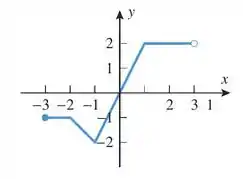
Passo 1

Vamos la, o domínio é de onde x começa ate onde x termina, pelo gráfico, conseguimos ver que ele começa em - 3 (incluindo ele) até 3 (sem incluir)

D = [ - 3,3 [

Agora a imagem é a mesma coisa só que para y

I = [ - 2,2 ]

Passo 2

Para achar f - 3 vamos olhar no gráfico onde temos a nossa função quando x = - 3 .

Colocando o dedo em - 3 no eixo x (o horizontal) vamos ver que y = - 1

Então temos que

f - 3 = - 1

Agora para f 1 2 , não conseguimos ver exaaatamente, mas se colocarmos o dedo na metade entre 0 e 1 , e chegando na curva, temos que a altura fica eme 1   no eixo y , então podemos dizer que

f 1 2 = 1

Passo 3

Para as soluções onde f ( x ) = - 3 2 , temos que f ( x ) = - 1,5   ou seja, o ponto no eixo y entre - 1 e - 2

A gente consegue ver que acontece em dois pontos

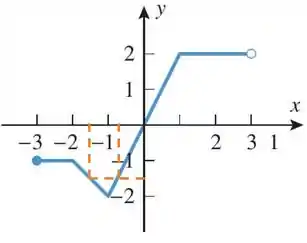
A gente consegue ver que fica em dois pontos,

x ≅ - 0,7

x ≅ - 1,5

Resposta

  1. O domínio de f é [ - 3,3 [
  2. A imagem de f é [ - 2,2 ]
  3. f ( - 3 ) = - 1
  4. f 1 2 = 1
  5. As soluções de f x = - 3 2 são x = - 0,7 e x = - 1,5
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine o domínio da função g ( x ) = l n | 4 - x 2 | .
Determine o domínio da função g ( x ) = e x + l n x .
Determine o domínio da função h ( x ) = l n ( c o s - 1 x ) .
Determine se f ( x ) = e l n | x | + 1 é par, ímpar, ou nenhuma das duas.
Determine se f ( x ) = | e x | é par, ímpar, ou nenhuma das duas.