Exercícios de Introdução às funções - Lista de Exercícios Resolvida
Questão 4
Abaixo, a função real de variável real é definida por sua expressão analítica. Determine o seu domínio.
Ver solução completaQuestão 5
Represente por diagrama de flechas e verifique se são funções de cada relação abaixo:
a) , sendo
b) sendo
Ver solução completaQuestão 8
Na superfície do oceano, a pressão da água é igual à do ar acima da água, . Para cada metro abaixo da superfície, a pressão da água cresce .
(a) Expresse a pressão da água como uma função da profundidade abaixo da superfície do oceano.
(b) A que profundidade a pressão é de .
Ver solução completaQuestão 13
- Considere a função
(c) Escreva como composta de duas funções mais simples.
Ver solução completaQuestão 16
Seja
(a) Determine o domínio da função
(b) Determine as equações das retas assíntotas horizontais do gráfico de , caso existam
(c) Determine as equações das retas assíntotas verticais do gráfico de , caso existam.
(d) Sabendo que é crescente em todo o seu domínio, esboce abaixo o gráfico de e suas retas assíntotas, caos existam.
Ver solução completaQuestão 18
Estabeleça o limite, encontrando para qualquer de maneira que a definição seja
válida.
Ver solução completaQuestão 23
5. Considere a função dada por e as seguintes afirmações
- é injetora
- é sobrejetora
- é inversível e sua inversa é dada por
- O gráfico de intercepta o eixo em apenas um valor
Quantas afirmações são verdadeiras:
Questão 24
10. Seja um número real positivo e considere as funções
Assinale a alternativa verdadeira
- Nenhuma das alternativas
Questão 27
Quando um projétil é lançado a uma velocidade formando um ângulo com a horizontal, seu alcance(isto é, a distância horizontal percorrida) é dada por
,
em que é a aceleração da gravidade. Se , qual deve ser o ângulo para que o alcance seja de ? Utilize
Ver solução completaQuestão 31
13. Sejam , e número reais e considere a função . Sabe-se que a imagem de é o intervalo e que os pontos e pertencem ao gráfico de . Então o produto é igual a
Questão 39
Dê o domínio e esboce o gráfico, enfatizando as características vistas em sala, de cada função.
a)
Ver solução completaQuestão 40
Dê o domínio e esboce o gráfico, enfatizando as características vistas em sala, de cada função.
c)
Ver solução completaQuestão 41
Dê o domínio e esboce o gráfico, enfatizando as características vistas em sala, de cada função.
d)
Ver solução completaQuestão 42
Dê o domínio e esboce o gráfico, enfatizando as características vistas em sala, de cada função.
b)
Ver solução completaQuestão 43
Dê o domínio e esboce o gráfico, enfatizando as características vistas em sala, de cada função.
e)
Ver solução completaQuestão 46
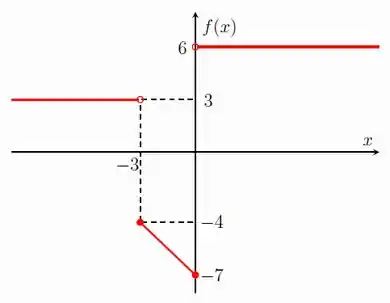
Seja . Responda
- Determine o domínio da função.
- Calcule .
- Calcule o valor de para que a função abaixo seja contínua em
Questão 47
Sejam e funções contínuas em , tais que e . Mostre que a equação tem solução.
Ver solução completaQuestão 48
Dê um exemplo (que pode ser gráfico) de uma função definida em tal que , mas não possui raiz em . O que se pode afirmar sobre a continuidade desta função?
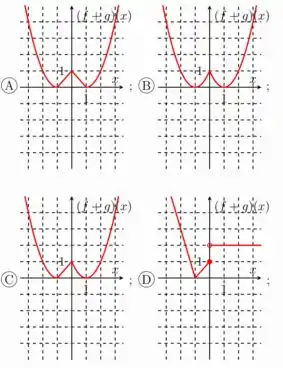
Ver solução completaQuestão 49
Seja e funções definidas por
O item que melhor representa o gráfico de é
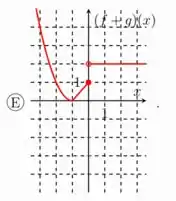
Questão 52
Diga quais das funções abaixo são injetoras, sobrejetoras ou bijetoras, considerando ℝ como contra-domínio para todas elas.
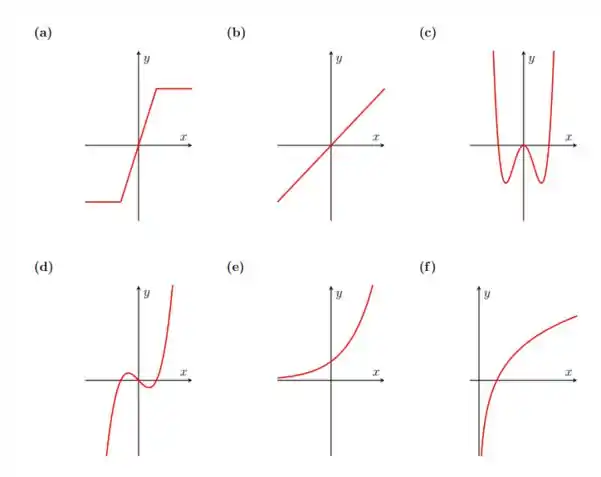
Questão 55
A reta intercepta os eixos coordenados nos pontos e . Determine a distância entre e , sabendo-se que passa pelos pontos e
Ver solução completaQuestão 58
8. Um retângulo é desenhado no 1° quadrante do plano cartesiano com a base sobre o eixo , um dos lados sobre o exido e o vértice restante sobre a reta .
Um exemplo de retângulo possível está representado na figura abaixo.
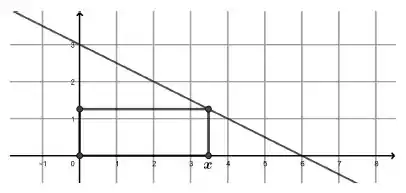
a) Encontre a função que calcula a área do retângulo em função do tamanho da base bem como seu domínio.
b) Determine a imagem da função encontrada no item anterior.
Ver solução completaQuestão 59
Sejam , e os lados de um triangulo retângulo, onde é a hipotenusa. Se o triângulo tem perímetro igual a , indique a área desse triangulo em função da hipotenusa.
Ver solução completaQuestão 60
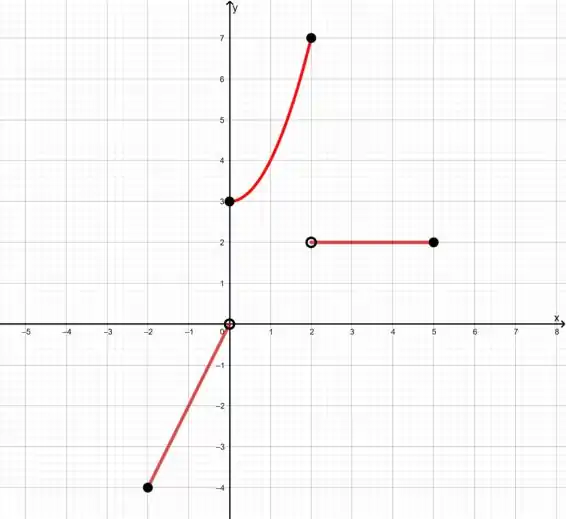
Considere a função abaixo
- Determine do domínio e a imagem da função acima
Questão 63
Estude o sinal (determine onde é positiva e onde é negativa) das funções
Ver solução completaQuestão 64
Estude o sinal (determine onde é positiva e onde é negativa) das funções
Ver solução completaQuestão 65
Estude o sinal (determine onde é positiva e onde é negativa) das funções
Ver solução completaQuestão 66
Estude o sinal (determine onde é positiva e onde é negativa) das funções
Ver solução completa
Questão 67
Estude o sinal (determine onde é positiva e onde é negativa) das funções
Ver solução completaQuestão 71
O governo estima que o custo, em milhares de reais, para despoluir de uma reserva de água doce é dado pela função
- Com base no texto, determine o domínio da função e o valor de .
Questão 72
Estude o sinal (determine onde é positiva e onde é negativa) das funções
Ver solução completaQuestão 75
Um cilindro fechado tem área de superfície fixa . Exprima seu volume como função do raio da base do cilindro.
Ver solução completaQuestão 76
O perímetro de um triângulo retângulo é e a hipotenusa é . Exprima a área do triângulo como função de .
Ver solução completaQuestão 77
5. Considere a função . Se é o intervalo que representa o domínio de , então é igual a
Questão 83
8. Um retângulo é desenhado no 1° quadrante do plano cartesiano com a base sobre o eixo , um dos lados sobre o exido e o vértice restante sobre a reta .
Um exemplo de retângulo possível está representado na figura abaixo.
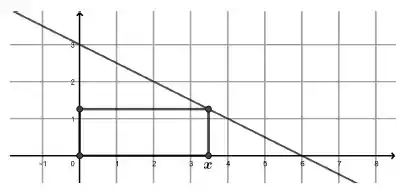
a) Encontre a função que calcula a área do retângulo em função do tamanho da base bem como seu domínio.
b) Determine a imagem da função encontrada no item anterior.
Ver solução completaQuestão 84
7. Considere a função definida em .
a) Determine a imagem de .
b) Determine
c) Determine a expressão da função inversa
Ver solução completa