O movimento de uma partícula no plano é descrito pelo sistema:
Desenhe a trajetória descrita pela partícula supondo que ela inicia o movimento na posição .
Passo 1
Escrevendo a equação na forma:
Temos:
Rearranjando:
Passo 2
Isolando as variáveis:
Integrando, obtemos:
Aplicando exponencial:
Passo 3
A partícula inicia o movimento em , então:
Desse modo:
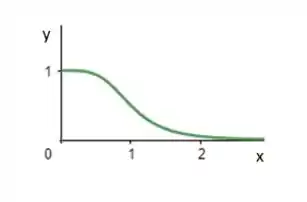
Obtendo um gráfico: