Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Cálculo - Anton - Cálculo - Vol 1- Ed: 10º - Capítulo 2.1 - Ex. 26

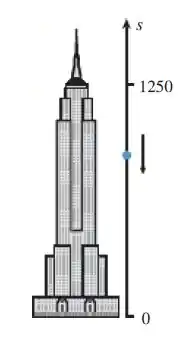
Suponha que um objeto seja largado do repouso (ou seja, com velocidade inicial nula) desde o alto do Empire State Building, em Nova Iorque, Estados Unidos, de uma altura de 1250 pés acima do nível da rua (ver Figura EX- 26 ). A altura do objeto (em pés) pode ser modelada pela função posição s = f t = 1250 - 16 t 2 .

  1. Verifique que o objeto ainda está caindo aos t = 5 s.
  2. Encontre a velocidade média do objeto no intervalo de t = 5 a t = 6 s.
  3. Encontre a velocidade instantânea do objeto no instante t = 5 s.

e

Passo 1

  1. Para verificar vamos substituir o valor de 5 na função, se o valor for maior que zero então quer dizer que o objeto ainda está caindo:

    2. f 5 = 1250 - 16 ⋅ 5 2 = 1250 - 16 ⋅ 25 = 850

    Pronto, f 5 > 0 então o objeto ainda está caindo.

    Passo 2

  2. Vamos achar a velocidade média do objeto no intervalo de t = 5 a t = 6 s da seguinte forma:

    3. m = f x 1 - f x 2 x 1 - x 2

    Vamos então achar os f dos pontos:

    f 5 = 85 0

    f 6 = 1250 - 16 ⋅ 6 2 = 1250 - 16 ⋅ 36 = 674

    Substituindo:

    m = v m e d = f x 1 - f x 2 x 1 - x 2 = 850 - 674 5 - 6 = 176 - 1 = - 176   p é s / s

    Passo 3

  3. A velocidade instantânea do objeto no instante t = 5 s é dada por:

v i n s t = lim h → 0 ⁡ f 5 + h - f 5 h

Vamos substituir f 5 + h e f 5 e calcular o limite:

v i n s t = lim h → 0 ⁡ f 5 + h - f 5 h = lim h → 0 ⁡ 1250 - 16 5 + h 2 - 850 h =

= lim h → 0 ⁡ 1250 - 16 25 + 10 h + h 2 - 850 h = lim h → 0 ⁡ 1250 - 400 - 1 6 0 h - 16 h 2 - 850 h =

= lim h → 0 ⁡ - 160 h - 16 h 2 h = lim h → 0 ⁡ - 160 - 16 h = - 160 - 16 ⋅ 0 = - 160   p é s / s

Resposta

b) v m e d = - 176   p é s / s

c) v i n s t = - 160   p é s / s

Ver Outros Exercícios desse livro