Enunciado
Cálculo - James Stewart - Vol 2- Ed: 8º - Capítulo 15.3 - Ex. 15
Utilize a integral dupla para determinar a área da região.
Um laço de rosácea .
Passo 1
Fala, pessoal! Tudo certo?
A questão pede para calcularmos a área de uma região usando uma integral dupla em coordenadas polares. Sabemos que área de uma região é dada por
Como em coordenadas polares , temos que
Primeiro, vamos precisar entender a qual região em coordenadas polares:
Corresponde nosso laço de rosácea.
Daí vamos tirar nossos limites de integração para as variáveis e , e vamos conseguir resolver nossa integral dupla.
E aí, para resolver nossa integral dupla, é só resolvermos “de dentro para fora”.
Vamos ver como fica essa resolução!
Passo 2
Neste caso, queremos a área de um laço da rosácea , que pode ser esquematizada na imagem abaixo:
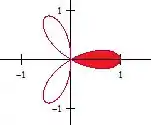
Quando pegamos ângulos partido do eixo , temos ângulos negativos, se pegarmos esses ângulos no sentido horário e ângulos positivos, se pegarmos no sentido horário.
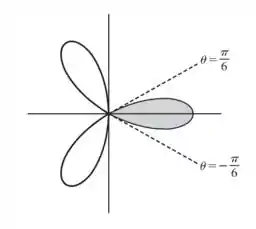
Um quadrante inteiro é , como nosso laço pega apenas 1/3 do quadrante, nosso intervalo será:
Quanto à ,o enunciado deu que:
Que é a distância radial do laço até a origem. Como o laço está centrado na origem, teremos:
Note que o primeiro valor é negativo, pois foi medido partindo do eixo no sentido horário.
Como o intervalo de integração de tem termo dependente de , colocarmos a integral “para dentro”, para facilitar nossa análise;
Passo 3
Vamos resolver nossa integral:
Vamos começar com a integral de dentro. Fazendo a integral em :
Tiramos a constante para fora e aplicamos o limite de integração:
Passo 4
Agora, sobra a integral de fora com o resultado da integral de dentro que acabamos de resolver:
Para facilitar a integração de , podemos fazer uma mudança de variáveis, prosseguir com a integração.
Fazendo a mudança , temos que
Substituindo na integral:
Multiplicando as constantes de fora:
Dessa forma, podemos ainda reescrever a integral, como:
A integral de de a é igual ao dobro da integral de de 0 a , porque é uma função par, ou seja, =. Isso permite que dividamos a integral simétrica em duas partes iguais.
Logo,
Usando a identidade trigonométrica:
Já separando como uma soma de integrais:
Aplicando os limites de integração:
Então: