Enunciado
Ciência dos Materiais - Callister - Ciência e Engenharia de Materiais. Uma Introdução- Ed: 8º - Capítulo 8.Problemas de Projetos - Ex. P2
(a) Para o tanque esférico de paredes finas que foi discutido no Exemplo de projeto , com base no critério do tamanho crítico da trinca [conforme abordado no item (a)], classifique os seguintes polímeros em ordem decrescente do comprimento crítico da trinca: nylon ( de umidade relativa), policarbonato, poli(etileno tereftalato) e poli(metil metacrilato). Comente a respeito da faixa de magnitudes dos valores calculados, usados para a classificação, em comparação com aqueles tabulados para as ligas metálicas na Tabela . Para esses cálculos, use os dados contidos nas Tabelas e no Apêndice .
(b) Agora, classifique esses mesmos quatro polímeros em relação à pressão máxima admissível de acordo com o critério de vazar antes de romper, conforme descrição no item (b) do Exemplo de Projeto . Da mesma forma que anteriormente, comente sobre esses valores em comparação aos relacionados para as ligas metálicas da Tabela .
Passo 1
Olá! Tudo bem? Vamos resolver esse problema em dois passos: item (a) no Passo e item (b) no Passo .
(a) Essa parte do problema exige que classifiquemos quatro polímeros em relação ao comprimento crítico da trinca na parede de um tanque esférico. No desenvolvimento do Exemplo de Projeto , foi observado que o comprimento crítico da trinca é proporcional ao quadrado da razão . Os valores de e , obtidos das Tabelas e , estão tabulados abaixo. (Nota: quando um intervalo de valores ou é fornecido, o valor médio é usado.)
Com base nesses valores, os quatro polímeros são classificados por quadrados da razão da seguinte maneira:
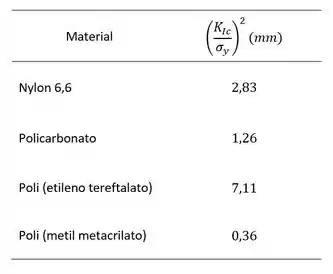
Esses valores são menores que os das ligas metálicas da Tabela , que variam de a .
Passo 2
(b) Em relação ao critério de vazamento antes da quebra, é usada a razão . Os quatro polímeros são classificados de acordo com os valores dessa relação da seguinte maneira:
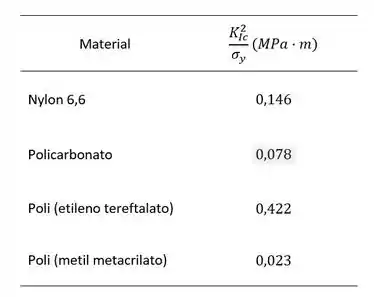
Esses valores são todos menores que os das ligas metálicas da Tabela , cujos valores variam de a .
Resposta
(a) Veja o Passo .
(b) Veja o Passo .