Usando os dados na Tabela 12.5, calcule a tensão crítica necessária para a propagação de uma trinca superficial com comprimento de 0.05mm, se a energia de superfície para um vidro de cal de soda é de .
Passo 1
Abaixo, a tabela 12.5 extraída do livro:
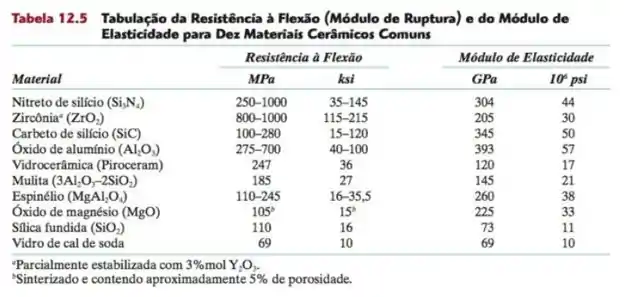
Agora, podemos determinar a tensão crítica necessária para a propagação de uma fissura superficial no vidro de soda-cal usando a Equação 8.3; considerando o valor de 69 GPa (Tabela 12.5) como módulo de elasticidade, obtemos: