Enunciado
Ciência dos Materiais - Callister - Ciência e Engenharia de Materiais. Uma Introdução- Ed: 8º - Capítulo 13.Perguntas e Problemas - Ex. 13
A viscosidade de um vidro varia com a temperatura de acordo com a relação
onde Qvis é a energia de ativação para o fluxo viscoso, A é uma constante independente da temperatura, e R e T são, respectivamente, a constante do gás e a temperatura absoluta. Um gráfico de ln η versus l/T deve ser quase linear, e com um declive de Qvis /R. Usando os dados da Figura 13.7, (a) fazer tal gráfico para o vidro borossilicato, e (b) determinar a energia de ativação entre as temperaturas de 500 e 900°C.
Passo 1
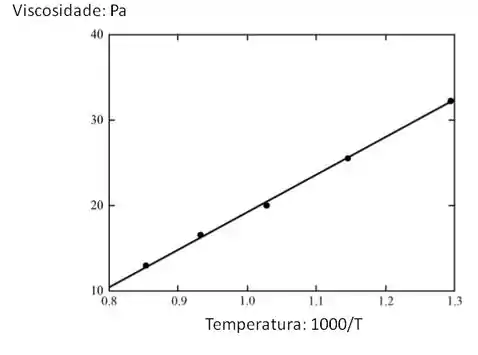
Certo galera, vamos lá! (a) Abaixo é mostrada a viscosidade do logaritmo versus o recíproco do gráfico de temperatura para o vidro borossilicato, usando os dados da Figura 13.7. A linha tracejada foi traçada através dos pontos de dados correspondentes a temperaturas entre 500 e 900ºC (conforme estipulado na declaração do problema).
Passo 2
(b) A energia de ativação, Qvis, pode ser computada de acordo com,
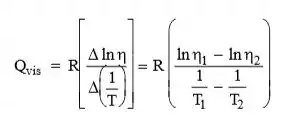
Pegando e como e , respectivamente, então os correspondentes valores de e serão e . Portanto,
