Fórmula de Capacitância

Opaa, seja muito bem vindo ao Responde Aí! Bora dar uma conferida na Fórmula da Capacitância?

📢 Clique para ver mais:

• Indutores
• Fórmulas de Capacitores
• Livros Resolvidos

O capacitor é um componente do circuito elétrico responsável por armazenar energia por alguns momentos para em seguida liberá-la em um só pulso, para ativar o Flash de uma câmera fotográfica. Mas… você sabe o que é capacitância?!

Capacitância

A capacitância está relacionada a quantidade de energia que um capacitor pode armazenar antes de liberar suas carga para um circuito elétrico! Podemos calculá-la com:

Onde:

• é a capacitância daquele capacitor medida em Farad ()
• é a quantidade de carga q ele consegue armazenar medida em Coulombs ()
• é o módulo da diferença de potencial a qual o capacitor está submetido

Para calcular a capacitância de um capacitor de acordo com sua forma, primeiro teremos que utilizar a Lei de Gauss, aquela integral de superfície fechada, que chamamos de Gaussiana para descobrir o campo elétrico do capacitor:

Que é o mesmo que:

Onde:

• é o vetor do campo elétrico
• é a forma vetorial da área
• é a quantidade de carga na parte interna da nossa superfície Gaussiana
• é a constante de permissividade do vácuo

Em seguida, a partir do campo elétrico, descobriremos p potencial elétrico naquela capacitor com:

Onde e são respectivamente o raio interno e o raio externo, é o campo elétrico que descobrimos com a Lei de Gauss e é o potencial elétrico.

Capacitância de um Capacitor Esférico

Vamos ver um exemplo para entender como calcular a capacitância de um capacitor em formato esférico conforme a figura:

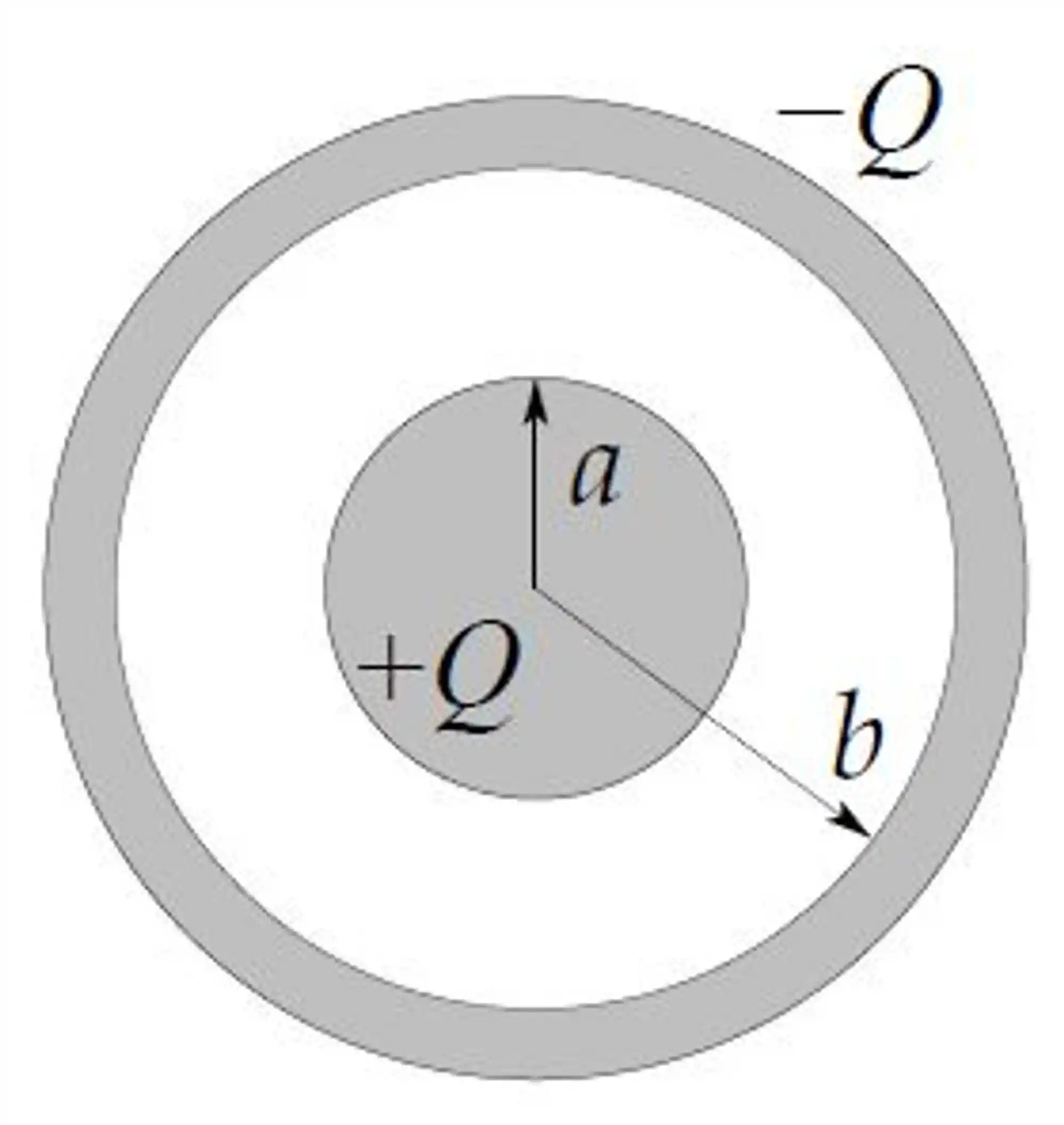
Temos uma situação de um capacitor esférico com uma placa interna esférica de raio e uma cobertura esférica externa de raio . Para manter a simetria do problema nossa superfície gaussiana terá de ser um esfera que envolva nosso capacitor. E por causa dessa simetria podemos simplificar a nossa integral sobre a superfície gaussiana de:

Para:

Onde calcularemos o campo elétrico, considerando a área como sendo a área de uma esfera:

Isolando como função de temos que:

Estamos analisando a região entre as esferas onde $a

Resolvendo essa integral:

E agora podemos calcular nossa capacitância:

Substituindo , descobrimos que a capacitância para o nosso capacitor esférico de raio interno e raio externo vale:

Que é o mesmo que:

Muita matemática né? Mas isso pode ser feito de maneira semelhante para capacitores de qualquer outra forma, como cilíndricos por exemplo, ou outros mais exóticos. Encontre tudo que precisa para passar na sua prova no nosso site.