Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Capacitores

Ver Todos os Exercícios

Teoria

Até agora a gente estudou circuitos que apresentavam apenas resistores. Agora vamos conhecer dois novos elementos passivos: o capacitor e o indutor. Começaremos pelo Capacitor.

O capacitor é projetado para armazenar energia em seu campo elétrico. Eles são muito utilizados em computadores e equipamentos eletrônicos e de comunicação.

Estrutura física

A sua estrutura física é composta por duas placas metálicas paralelas de área A separadas por um dielétrico.

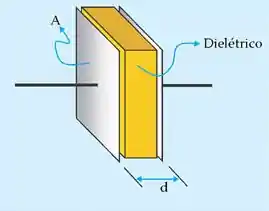
Agora, vamos ver o que acontece quando conectamos uma fonte de tensão nos terminais do capacitor:

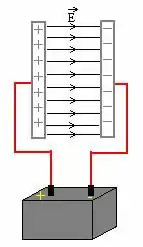
Quando a gente faz isso, uma placa fica carregada com uma carga q positiva, enquanto a outra fica carregada negativamente com uma carga – q . Dizemos, então, que o capacitor está carregado e que o total de carga armazenado ( q ) é diretamente proporcional à tensão v aplicada.

q = C v

Onde C é chamada de capacitância e é medida em farads (F).

Relembrando que q é medido em coulomb e v em volts. Então, pela equação, temos que 1 farad = 1 coulomb/volt.

Capacitância

Como a gente viu pela equação acima, a capacitância é a razão entre a carga que está armazenada no capacitor pela diferença de potencial entre as suas placas. Mas apesar disso tudo, ela não depende de q ou v , e sim das dimensões físicas do capacitor.

Por exemplo, vamos olhar a estrutura do capacitor novamente:

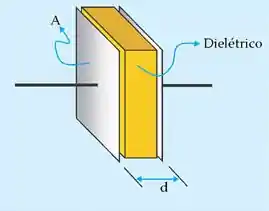
O valor da capacitância para esse capacitor pode ser obtido pela relação:

C = є   A d

Onde A   → á r e a   d a   s u p e r f í c i e   d e   c a d a   p l a c a                                                                                     d   → d i s t â n c i a   e n t r e   a s   p l a c a s                                                                                                                       є   → p e r m i s s i v i d a d e   d o   m a t e r i a l   d i e l é t r i c o   e n t r e   a s   p l a c a s

Apesar dessa equação se aplicar somente em capacitores de placas paralelas, a gente pode concluir que basicamente três fatores determinam o valor da capacitância:

  1. A área da superfície das placas;
  2. O espaçamento entre as placas;
  3. A permissividade do material do dielétrico.

Enquanto a área A e a distância entre as placas d são características construtivas do capacitor, a permissividade ε é uma propriedade do material utilizado entre as placas, que chamamos de dielétrico.

Tipos e valores típicos

Os capacitores geralmente são representados no circuito com a simbologia abaixo:

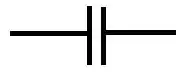
Eles normalmente são comercializados na faixa de picofarad (pF) a microfarad (µF) e podem ser de:

Poliéster:

Cerâmica:

Eletrolítico:

Relação corrente-tensão

Para encontrar a relação corrente-tensão no capacitor, partimos da nossa primeira equação:

q = C v

Agora a gente deriva os dois lados da equação em relação ao tempo:

d q d t = d ( C v ) d t

Como

i = d q d t

e como C é uma constante, temos:

i = C d v d t       ( i )

Pronto, essa é a relação entre corrente e tensão em um capacitor, sempre lembrando que o capacitor é um elemento passivo. Então, ele possui a mesma convenção que usamos para resistor:

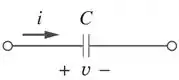
Se quisermos isolar a tensão na equação ( i ) precisamos integrar os dois lados da equação, obtendo:

v = 1 C ∫ - ∞ t i   d t + v t 0

Onde

v t 0 = q t 0 C

É a tensão no capacitor no tempo t 0 .

Sabendo essas relações podemos obter as equações de potência e energia de um capacitor.

Para potência, temos:

P = v i

P = v   C d v d t

Logo, a energia armazenada será:

w = ∫ - ∞ t P   d t

w = ∫ - ∞ t   v   C d v d t d t

w =   C ∫ - ∞ t v   d v

w = 1 2 C v 2

Antes de estudarmos associação de capacitores, vamos ver algumas propriedades interessantes do capacitor a partir da equação ( i ) .

i = C d v d t       ( i )

A primeira é que um capacitor é um circuito aberto para tensão contínua. Isso acontece porque quando a tensão não varia em relação ao tempo, a corrente que passa pelo capacitor é zero.

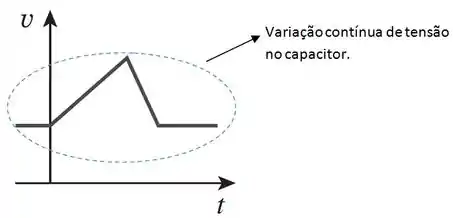
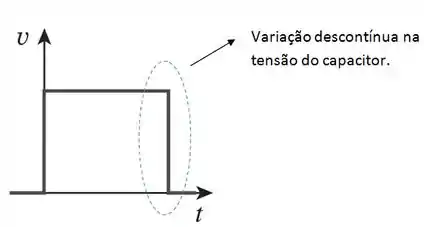
A segunda propriedade é que a tensão no capacitor não pode variar instantaneamente, porque uma variação descontínua na tensão requer uma corrente infinita, que é fisicamente impossível.

Vamos dar uma olhada nos gráficos abaixo para entender melhor:

Tensão permitida em um capacitor:

Tensão não permitida em um capacitor:

Associação de Capacitores

Vamos supor que a gente tenha o circuito abaixo, com os capacitores associados em paralelo:

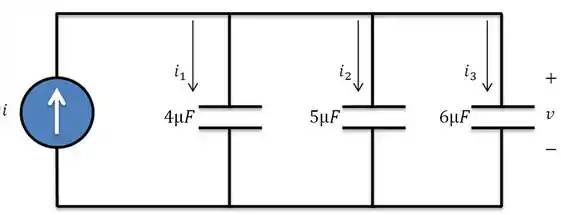
Aplicando a LCK:

i = i 1 + i 2 + i 3

Pela relação de corrente no capacitor:

i 1 = 4 µ d v d t

i 2 = 5 µ d v d t

i 3 = 6 µ d v d t

Substituindo:

i = 4 µ d v d t + 5 µ d v d t + 6 µ d v d t

i = 4 µ + 5 µ + 6 µ d v d t  

i = 15 µ d v d t  

Logo,

C e q = 4 µ + 5 µ + 6 µ = 15 µ F

Então, quando os capacitores estão em paralelo, a capacitância equivalente é a soma das capacitâncias de cada capacitor.

C e q = C 1 + C 2 + C 3 + … + C N

Agora, vamos ver para o caso dos capacitores associados em série. Como no circuito abaixo:

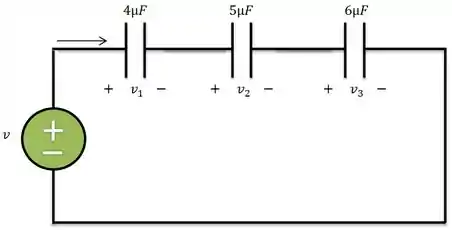
Aplicando LTK no circuito:

v = v 1 + v 2 + v 3

Pela relação de tensão no capacitor:

v 1 = 1 4 µ   ∫ - ∞ t i t d t + v 1 ( t 0 )  

v 2 = 1 5 µ   ∫ - ∞ t i t d t + v 2 ( t 0 )

v 3 = 1 6 µ   ∫ - ∞ t i t d t + v 3 ( t 0 )

Substituindo:

v = 1 4 µ   ∫ - ∞ t i t d t + v 1 ( t 0 ) + 1 5 µ   ∫ - ∞ t i t d t + v 2 ( t 0 ) + 1 6 µ   ∫ - ∞ t i t d t + v 3 ( t 0 )

v = 1 4 µ + 1 5 µ + 1 6 µ ∫ - ∞ t i t d t + v 1 ( t 0 ) + v 2 t 0 + v 3 t 0

v = 37 60 µ ∫ - ∞ t i t d t + v ( t 0 )

Logo,

1 C e q = 1 4 µ + 1 5 µ + 1 6 µ = 37 60 µ

Então, quando os capacitores estão associados em série, a capacitância equivalente é o inverso da soma dos inversos das capacitâncias de cada capacitor.

1 C e q = 1 C 1 + 1 C 2 + 1 C 3 + … + 1 C N

Puxando na memória, a gente nota que os capacitores em série se associam da mesma forma que os resistores em paralelo. Então, para a associação de dois capacitores temos aquela velha fórmula do produto sobre a soma:

C e q = C 1 C 2 C 1 + C 2

Muita coisa nova, hein! Mas calma que eu vou fazer um resumão maneiro aqui!

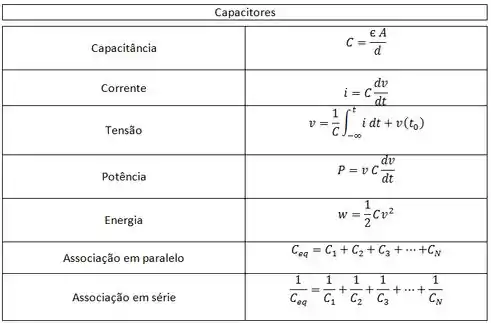
Agora é praticar bastante!

Tipos e valores típicos

Relação corrente-tensão

Associação de Capacitores

Exercícios Resolvidos

Exercício Resolvido #1

Introdução à análise de circuitos – Robert L. Boylestad – Ed. 12 – Exercício 10.3

Determine a capacitância de um capacitor de placas paralelas se 1200µC de carga se acumulam em suas placas quando a tensão aplicada é de 24V.

Passo 1

Pelo que sabemos, temos a fórmula:

q = C * V

Onde a carga q dada no enunciado é igual ao produto da capacitância C e a tensão aplicada V .

Logo,

1200 µ C = C * 24 V

C = 1200 µ C 24 V = 50 µ F  

Resposta

C = 50 µ F

Exercício Resolvido #2

Livro Sadiku, 5ª edição, p.214, Problema 6.1

Se a tensão em um capacitor de 7,5   F   for de 2 t e - 3 t   V , determine a corrente e a potência.

Passo 1

Primeiro, vamos ver os dados que o enunciado nos fornece:

C = 7,5   F

v = 2 t e - 3 t   V

Passo 2

Agora vamos calcular a corrente. Sabemos que a corrente em um capacitor tem a seguinte relação:

i = C d v d t  

Substituindo os dados do enunciado:

i = 7,5 d d t 2 t e - 3 t

Passo 3

Precisamos resolver a derivada. Pela regra do produto, temos:

d d t 2 t e - 3 t = 2 e - 3 t + ( - 3 e - 3 t 2 t )

d d t 2 t e - 3 t = 2 e - 3 t - 6 t e - 3 t

Passo 4

Agora, vamos substituir na equação da corrente.

i = 7,5 2 e - 3 t - 6 t e - 3 t

i = 15 1 - 3 t e - 3 t   A

Passo 5

Falta determinarmos a potência. Sabemos que:

P = v i

Substituindo os valores:

P = 2 t e - 3 t 15 1 - 3 t e - 3 t

P = 30 t e - 3 t 1 - 3 t e - 3 t

P = 30 t 1 - 3 t e - 6 t   W

Resposta

i = 15 1 - 3 t e - 3 t   A

P = 30 t 1 - 3 t e - 6 t   W

Exercício Resolvido #3

Livro Sadiku, 5ª edição, p.214, Problema 6.2

Um capacitor de 50 μ F possui energia w t = 10 cos 2 ⁡ ( 377 t )   J . Determine a corrente que passa pelo capacitor.

Passo 1

O enunciado nos fornece os seguintes dados:

C = 50 μ F

w t = 10 cos 2 ⁡ ( 377 t )   J

E pede a corrente, que possui a seguinte relação no capacitor:

i = C d v d t  

Passo 2

Precisamos encontrar a tensão nesse capacitor para podermos substituir na fórmula da corrente. A gente tem a seguinte relação para energia em um capacitor:

w = 1 2 C v 2

Substituindo os valores dados no enunciado na fórmula da energia:

10 cos 2 ⁡ ( 377 t ) = 1 2 ( 50 μ ) v 2

Isolando v :

v 2 = 20 50 × 10 - 6 c o s 2 377 t

v 2 = 400000 c o s 2 377 t

v = ± 400000 c o s 2 377 t

Escolhendo v positivo:

v ( t ) = 632,45 cos ⁡ 377 t V

Passo 3

Agora, vamos substituir o valor encontrado para tensão na equação da corrente:

i = C d v d t

i = 50 × 10 - 6 d d t 632,45 cos ⁡ 377 t

i = 50 × 10 - 6 632,45 - 377 s i n 377 t

i t = - 11,93 sin ⁡ 377 t A

Resposta

i t = - 11,93 sin ⁡ 377 t A

Exercício Resolvido #4

Livro Sadiku, 5ª edição, p.214, Problema 6.4

Uma corrente de 4 sen ⁡ ( 4 t )   A passa por um capacitor de 5   F . Descubra a tensão v t no capacitor dado que v 0 = 1   V .

Passo 1

Primeiro, vamos ver os dados que o enunciado nos fornece:

i ( t ) = 4 s e n ( 4 t )

C = 5   F

v 0 = 1   V

Além disso:

t 0 = 0

Passo 2

Agora, vamos lembrar a equação da tensão no capacitor:

v t = 1 C ∫ - ∞ t i t d t + v ( t 0 )

Substituindo os valores dados no enunciado:

v t = 1 5 ∫ 0 t 4 s e n 4 t   d t + v ( 0 )

v t = 1 5 ∫ 0 t 4 s e n 4 t   d t + 1

Passo 3

Precisamos resolver aquela integral. Vamos resolver usando substituição simples.

u = 4 t   d u = 4   d t

∫ 4 s e n u d u 4

∫ s e n u d u   =   - c o s ⁡ ( u )

Voltando:

∫ 0 t 4 s e n 4 t   d t = - c o s ⁡ ( 4 t ) t 0

∫ 0 t 4 s e n 4 t   d t = - cos ⁡ 4 t + c o s ⁡ ( 0 )

∫ 0 t 4 s e n 4 t   d t = - cos ⁡ 4 t + 1

Passo 4

Agora, vamos substituir o resultado da integral na equação da tensão:

v t = 1 5 - cos ⁡ 4 t + 1 + 1

Logo:

v t = - 0,2 cos ⁡ 4 t + 0,2 + 1

v t = - 0,2 cos ⁡ 4 t + 1,2

Resposta

v ( t ) = 1,2 - 0,2 cos ⁡ 4 t   V

Exercício Resolvido #5

Livro Sadiku, 5ª edição, p.214, Problema 6.8

Um capacitor de 4 m F apresenta a seguinte tensão em seus terminais:

v =   50   V ,                                                                                           t ≤ 0   A e - 100 t + B e - 600 t       V ,                       t ≥ 0

Se o capacitor tiver uma corrente inicial de 2   A , determine:

  1. As constantes A e B .
  2. A energia armazenada no capacitor em t = 0 .
  3. A corrente no capacitor para t > 0 .

Passo 1

Vamos começar! O enunciado nos fornece a corrente em t = 0 :

i 0 = 2   A

Sabemos que a corrente no capacitor tem a seguinte relação:

i = C d v d t

Para t ≥ 0 , temos:

i = C d d t A e - 100 t + B e - 600 t

Passo 2

Resolvendo a derivada:

i ( t ) = C ( - 100 A e - 100 t - 600 B e - 600 t )

Quando, t = 0 :

i 0 = - 100 C A - 600 C B

Como, i 0 = 2   A e C = 4 × 10 - 3 F :

2 = - 0,4 A - 2,4 B

Passo 3

Precisamos de mais uma equação que relacione A e B . Então, vamos analisar a tensão no capacitor. Nós vimos na teoria que a tensão no capacitor não pode variar instantaneamente. Logo:

v 0 - = v 0 +

Pelo enunciado, sabemos que v 0 - = 50   V . Para v 0 + , temos:

v 0 + = A e - 100 ( 0 ) + B e - 600 ( 0 )

v 0 + = A + B

Logo, nossa segunda relação é:

50 = A + B

Passo 4

Então, vamos resolver o sistema abaixo para encontrarmos A e B :

A + B = 50 - 0,4 A - 2,4 B = 2

Isolando B na primeira equação e substituindo na segunda, temos:

- 0,4 A - 2,4 50 - A = 2

Simplificando:

2 A = 122

A = 61

Logo:

B = 50 - 61

B = - 11

Passo 5

A letra b) pede a energia do capacitor em t = 0 . A gente sabe que a energia no capacitor tem a seguinte relação:

w = 1 2 C v 2

Já vimos que v 0 = 50   V . Logo:

w = 1 2 4 × 10 - 3 50 2

w = 5   J

Passo 6

Vimos no início do exercício que a equação para corrente é a seguinte:

i ( t ) = C ( - 100 A e - 100 t - 600 B e - 600 t )

Como:

C = 4 m F

A = 61

B = - 11

Substituindo:

i t = 4 × 10 - 3 ( - 100 61 e - 100 t - 600 - 11 e - 600 t )

i t = - 24,4 e - 100 t + 26,4 e - 600 t   A

Resposta

a )   A = 61 ; B = - 11

b )   w = 5   J

c )   i t = - 24,4 e - 100 t + 26,4 e - 600 t   A

Exercício Resolvido #6

Livro Sadiku, 5ª edição, p.215, Problema 6.13

Determine a tensão nos capacitores do circuito da figura abaixo em CC.

Passo 1

A gente viu na teoria que os capacitores em corrente contínua funcionam como circuitos abertos. Logo, temos o circuito abaixo:

Passo 2

A corrente só circula em caminhos fechados. Logo, ela não passa pelo resistor de 50   Ω e a tensão v 2 e v 1 podem ser obtidas conforme o circuito abaixo:

Aplicando divisor de tensão, temos:

v 1 =   40 40 + 10 + 20 60

v 1 = 34,3   V

Passo 3

A tensão v 2 é igual à tensão da fonte diminuída da tensão no resistor de 20   Ω , que vamos chamar de v 3 , ou seja:

v 2 = 60 - v 3

Por divisor de tensão, temos:

v 3 = 20 40 + 10 + 20 60

v 3 = 17,1   V

Logo:

v 2 = 60 - 17,1

v 2 = 42,9   V

Resposta

v 1 = 34,3   V

v 2 = 42,9   V

Exercício Resolvido #7

Introdução à análise de circuitos – Robert L. Boylestad – Ed. 12 – Exercício 10.47

Calcule a capacitância total C T para o circuito da figura:

Passo 1

Vemos que os capacitores de 8µF e o de 12µF estão em paralelo, logo a capacitância equivalente entre eles é:

C e q = 8 + 12 = 20 µ F

Passo 2

Podemos ver que os capacitores de 6µF e 4µF estão em paralelo, logo a capacitância equivalente entre eles é:

C e q = 6 + 4 = 10 µ F

Passo 3

A capacitância total é o circuito série entre essas duas capacitâncias equivalentes já calculadas:

C T = 10 * 20 10 + 20 = 6,67 µ F

Resposta

C T = 6,67 µ F

Exercício Resolvido #8

Livro Sadiku, 5ª edição, p.215, Problema 6.16

A capacitância equivalente nos terminais a - b no circuito abaixo é 30 μ F . Calcule o valor de C .

Passo 1

Vamos calcular a Capacitância equivalente nos terminais a - b . Primeiro, vamos calcular a capacitância equivalente dos capacitores em série e vamos chamá-la de C e q 1 .

Com capacitores é o inverso do que a gente fazia com resistores. Como eles estão em série, temos:

C e q 1 = C × 80 µ C + 80 µ

Passo 2

Agora, como eles estão em paralelo é só somar para encontrarmos a C e q nos terminais a - b .

C e q = 14 µ + C × 80 µ C + 80 µ

Passo 3

O enunciado nos disse o valor de C e q é 30 µ F . Então vamos substituí-lo na equação acima e encontrar C .

30 µ = 14 µ + C × 80 µ C + 80 µ

30 µ - 14 µ = C × 80 µ C + 80 µ

16 µ = C × 80 µ C + 80 µ

16 µ C + 80 µ = 80 µ C

Simplificando:

16 C + 80 µ = 80 C

16 C + 1280 µ = 80 C

64 C = 1280 µ

C = 1280 64 µ

C = 20 µ F

Resposta

C = 20 µ F

Exercício Resolvido #9

Livro Sadiku, 5ª edição, p.215, Problema 6.19

Determine a capacitância equivalente entre os terminais a - b no circuito da figura abaixo. Todas as capacitâncias se encontram em μ F .

Passo 1

Vamos começar do final do circuito. Os capacitores de 10 ,   20 e 30 estão em paralelo. Então, basta somar as capacitâncias:

C e q 1 = 10 + 20 + 30 = 60 µ F

Passo 2

Agora, ficamos com o capacitor de 50 em paralelo com a associação em série dos capacitores de 60.

C e q 2 = 50 + 60 × 60 60 + 60

C e q 2 = 50 + 30 = 80 µ F

Passo 3

Fazendo a capacitância equivalente dos capacitares de 80 e 40 , que estão em paralelo:

C e q 3 = 80 + 40 = 120 µ F

Passo 4

Os capacitores C e q 3 e C e q 2 estão em série. Logo:

C e q 4 = 120 × 80 120 + 80

C e q 4 = 48 µ F

Passo 5

Vamos fazer a associação em paralelo:

C e q 5 = 12 + 48 = 60 µ F

Passo 6

Pronto, agora é só fazer a associação em série dos capacitores.

C e q = 12 × 60 12 + 60 = 10 µ F

Resposta

C e q = 10 µ F

Exercício Resolvido #10

Livro Sadiku, 5ª edição, p.217 Problema 6.32

No circuito da figura abaixo, seja i s = 50 e - 2 t   m A e v 1 0 = 50   V , v 2 0 = 20   V . Determine:

(a)     v 1 t e v 2 t

(b) a energia em cada capacitor em t = 0,5   s .

Passo 1

Vamos começar. A tensão em um capacitor tem a seguinte relação:

v t = 1 C ∫ - ∞ t i t d t + v ( t 0 )

Logo, para a tensão v 1 , temos:

v 1 ( t ) = 1 12 × 10 - 6 ∫ 0 t 50 e - 2 t × 10 - 3   d t + v 1 0  

v 1 ( t ) = 50 × 10 - 3 12 × 10 - 6 ∫ 0 t e - 2 t   d t + 50

v 1 ( t ) = 4166,67 ∫ 0 t e - 2 t   d t + 50

Passo 2

Vamos resolver a integral separadamente. Utilizando substituição simples, temos:

∫ 0 t e - 2 t   d t

u = - 2 t d u = - 2 d t

Substituindo:

- 1 2 ∫ e u d u   = - 1 2 e u

Voltando para t :

∫ 0 t e - 2 t   d t = - 1 2 e - 2 t t 0

∫ 0 t e - 2 t   d t = - 1 2 ( e - 2 t - 1 )

Passo 3

Substituindo o resultado da integral na equação de v 1 t :

v 1 t = 4166,67 - 1 2 e - 2 t - 1 + 50

v 1 t = - 2083,33 e - 2 t + 2133,33   V

Passo 4

Para calcular v 2 t , primeiro vamos calcular a capacitância equivalente entre os capacitores de 20 µ F e 40 µ F que estão em paralelo.

C e q = 20 + 40 = 60 µ F

Logo, temos o seguinte circuito:

Passo 5

Então, vamos encontrar v 2 ( t ) .

v 2 t = 1 60 × 10 - 6 ∫ 0 t 50 e - 2 t × 10 - 3   d t + v 2 0

v 2 ( t ) = 50 × 10 - 3 60 × 10 - 6 ∫ 0 t e - 2 t   d t + 20

v 2 ( t ) = 833,33 ∫ 0 t e - 2 t   d t + 20

Já calculamos essa integral ali em cima. Substituindo o seu resultado:

v 2 t = 833,33 - 1 2 e - 2 t - 1 + 20

v 2 t = - 416,67 e - 2 t + 436,67   V

Passo 6

Agora, a gente precisa encontrar a energia de cada capacitor no instante t = 0,5   s . A relação da energia em um capacitor é a seguinte:

w = 1 2 C v 2

Passo 7

Primeiro, vamos calcular as tensões em t = 0,5   s .

Para v 1 :

v 1 0,5 = - 2083,33 e - 2 0,5 + 2133,33

v 1 0,5 = - 766,41 + 2133,33

v 1 0,5 = 1366,92   V

Para v 2 :

v 2 0,5 = - 416,67 e - 2 ( 0,5 ) + 436,67  

v 2 0,5 = - 153,28 + 436,67

v 2 0,5 = 283,39   V  

Passo 8

Vamos dar uma olhada no circuito.

No capacitor de 12 µ F está sendo aplicada a tensão v 1 . Logo, a energia nele em t = 0,5   s , será:

w 12 µ = 1 2 12 × 10 - 6 1366,92 2

w 12 µ = 11,21   J

Como os capacitores de 20 µ F e 40 µ F estão ligados em paralelo, a mesma tensão v 2 está sendo aplicada nos dois capacitores. Logo:

w 20 µ = 1 2 20 × 10 - 6 283,39 2 = 0,803   J

w 40 µ = 1 2 40 × 10 - 6 283,39 2 = 1,606   J

Resposta

a )       v 1 t = - 2083,33 e - 2 t + 2133,33   V v 2 t = - 416,67 e - 2 t + 436,67   V        

b )   w 12 µ = 11,21   J w 20 µ = 0,803   J w 40 µ = 1,606   J

Exercícios de Livros Relacionados

O pulso de corrente de formato retangular mostrado na Figura P6.21 é aplicado a um capacitor de 0,1 mF. A tensão inicial no capacitor é uma queda de 15 V na direção de referência da corrente. Deduza a
A capacitância total de dois capacitores de 40m F em série associada em paralelo com um capacitor de 4m F é igual a:3,8 mF5 mF24 mF44 mF84 mF
Na figura abaixo, se i = cos ⁡ 4 r e v = sin ⁡ 4 r , o compomente é um:resistorcapacitorindutor
Para o circuito da figura abaixo, a fórmula para o divisor de tensão é: V 1 = L 1 + L 2 L 1 V s V 1 = L 1 + L 2 L 2 V s V 1 = L 2 L 1 + L 2 V s V 1 = L 1 L 1 + L 2 V s
Uma tensão CC de 10V é aplicada a um integrador com R = 50 k Ω , C = 100 μ F em t = 0 . Quanto tempo levará para o amplificador operacional saturar se as tensões de saturação forem + 12 V e - 12 V ? S