2- Se , o valor de é:

1

2

O valor de pode ser calculado por:

E a função (que é periódica) dada no enunciado pode ser representado da seguinte forma:

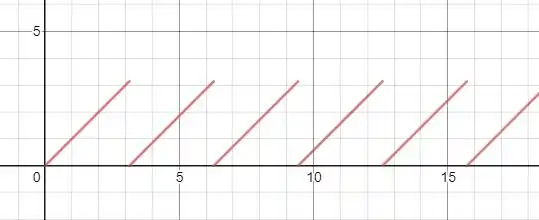
Pois é a união de várias retas no domínio de , é isso que a recursividade nos diz. Já que então temos uma reta com um domínio começando em não . Ou seja:

Em outras palavras temos as seguintes retas:

Com inteiro.

Isso serve para nos dizer que o período dessa função é:

Então:

Nos dando letra