Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 16.Problemas - Ex. 89
Desenvolva as equações de estado para o circuito apresentado na Figura
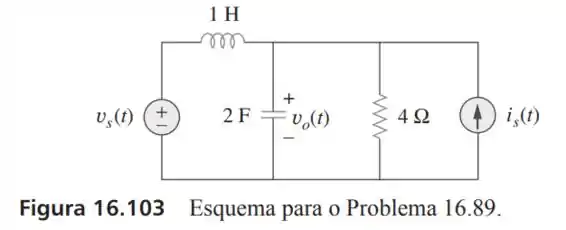
Passo 1
As variáveis de estado serão a tensão no capacitor e a corrente no indutor . Pois são as variáveis mais fáceis de escrever as suas derivadas no tempo.
As variáveis de entrada são as fontes e que valem e .
Como nós conseguimos escrever a equação de saída:
Então :
Passo 2
Agora a equação de estado deverá ter a seguinte forma:
E com isso vamos escrever cada variável do nosso problema no circuito:
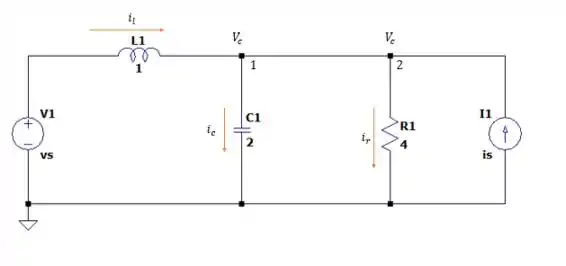
Por terem a mesma tensão , podemos dizqer que os nós e são iguais, então podemos dizer que as correntes que entram nesses nós são iguais com as que saem ou seja:
E essa equação pode ser escrita como:
Isolando a derivada temos:
A corrente que passa no indutor será pela diferença de tensão entre e :
Com as duas derivadas primeiras estando explícitas podemos escrever a equação: