Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 17.Problemas - Ex. 10

10- Determine a série de Fourier exponencial para a forma de onda da Figura 17.53

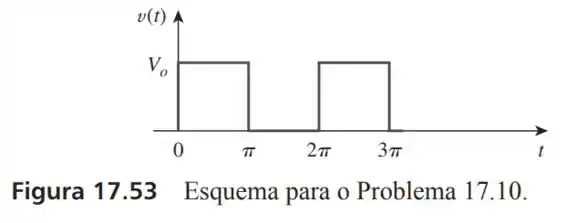
Passo 1

O período dessa onda vale T = 2 π , logo ω = 1 pois ω = 2 π T .

Onde para 0 < t < π temos v t = V o

A forma exponencial da série de Fourier é:

v t = ∑ n = - ∞ ∞ c n e j n ω o t

Onde :

c n = 1 T ∫ 0 T v t e - j   n ω o t d t

Passo 2

Então temos a seguinte integral para c n :

c n = 1 2 π ∫ 0 π V o e - j n t   d t

Fazendo essa integral temos:

c n = 1 2 π × 1 - j n V o e - j n t   0 π

c n = V o - j 2 π n [ e - j n π - 1 ]

Multiplicando por j em cima e embaixo temos:

c n = j V o 2 π n e - j n π - 1

Só que pela identidade de Euler sabemos que:

e j x = cos ⁡ x + j s i n   x

Então para x = - n π

e - j n π = cos ⁡ ( - n π ) + j s i n ( - n π )

Como n é um número inteiro e cosseno é uma função par temos:

e - j n π = cos ⁡ n π + j 0

Logo:

c n = j V o 2 π n c o s ⁡ ( n π ) - 1

Passo 3

Então a série de Fourier exponencial será:

v t = ∑ n = - ∞ ∞ c n e j n ω o t

v t = ∑ n = - ∞ ∞ j V o 2 π n c o s ⁡ ( n π ) - 1 e j n t

Resposta

v t = ∑ n = - ∞ ∞ j V o 2 π n c o s ⁡ ( n π ) - 1 e j n t

Ver Outros Exercícios desse livro