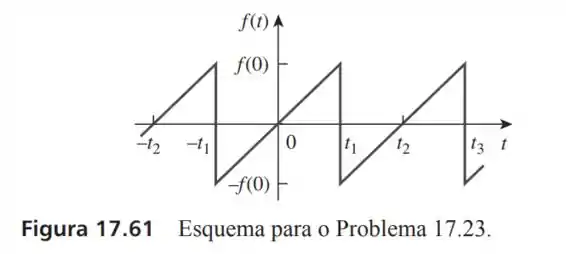
23- Considere a Figura e elabore um problema para ajudar outros estudantes a entender melhor como determinar as série de Fourier de uma forma de onda periódica.
Passo 1
Vamos considerar e . E queremos encontrar a forma da série de Fourier dessa onda triangular aí.
Essa onda é tem duas simetrias, a de meia onda, pois a mesma parcela em baixo da reta do tempo encontra-se invertida na parte de cima e é uma função ímpar também, pois:
Então por ser ímpar:
E por ser simetrica de meia onda:
Então basta encontrar sabendo que no período de até a onda tem o seguinte comportamento:
Pois quando
E como o período dessa onda é de logo :
Não escolhi o valor de a toa hahah
Passo 2
Então podemos calcular da seguinte maneira:
Essa integral é uma integral que se faz por partes e sabemos que:
Então:
Então:
Onde para qualquer inteiro:
Então:
Só que , já que cada número inteiro de faz essa função somente mudar o sinal então com o sinal negativo de teremos:
Passo 3
Como é a parte que se liga com o seno então temos a seguinte série de Fourier:
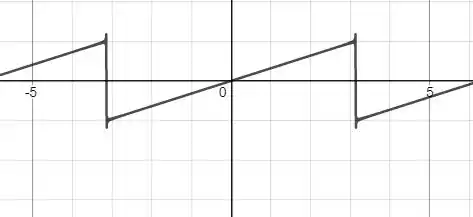
E isso nos dá o seguinte gráfico.