27- Para a forma de onda mostrada na Figura a seguir,
Especifique o tipo de simetria que ela possui
Calcule e
Determine o valor usando os cinco primeiros harmônicos não nulos
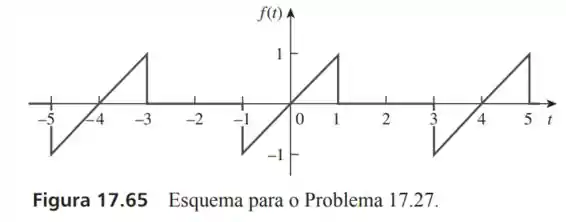
Passo 1
Pela onda a cima da linha horizontal ser invertida com a parte de baixo então a onda tem simetria de meia onda. Nos dando:
E por por exemplo nós conseguimos ver uma simetria de função ímpar, ou seja
Agora utilizando somente metade do período dessa onda nós temos:
Onde
Passo 2
Dessa forma o valor de será:
Fazendo a integração por partes temos:
Com então temos o seguinte resultado ao aplicar o intervalo:
Onde para qualquer inteiro e nós teremos para ímpar:
E para par:
Pois .
Então temos que utilizar os valores ímpares e pares de .
Portanto será:
Plotando o gráfico da série de Fourier :
Nós vamos ter:
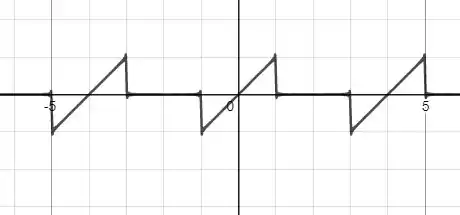
Passo 3
O valor de uma série de Fourier é descoberto fazendo:
Onde é a parte (contínua) e e é a parte (alternada)
Como não temos e nem então vamos calcular os cinco termos de.
Logo: