26- Encontre a representação da série de Fourier do sinal mostrado na Figura
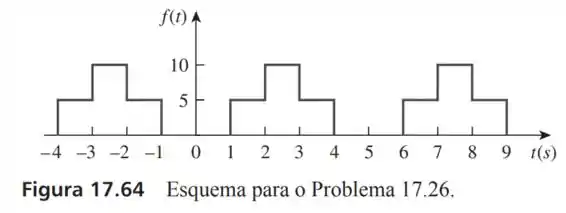
Passo 1
Podemos ver no sinal do meio que o período desse sinal vai de até nos dando um período de:
Portando:
E a onda tem o seguinte comportamento:
Passo 2
Portanto será:
Passo 3
Agora será:
Passo 4
Agora para calcular :
Passo 5
Isso nos dá a seguinte série de Fourier.
Nos dando o seguinte gráfico.
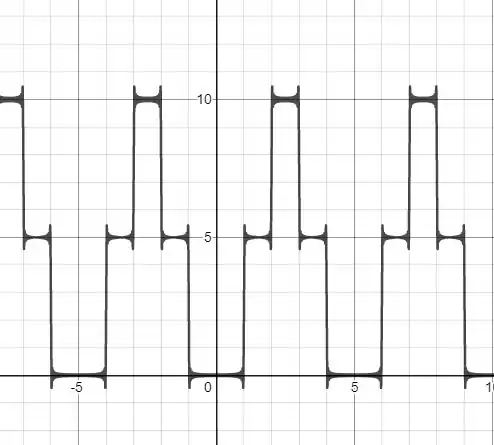
Trabalhoso, mais deu certo!