29- Determine a expansão da série de Fourier da função onda dente de serra da Figura
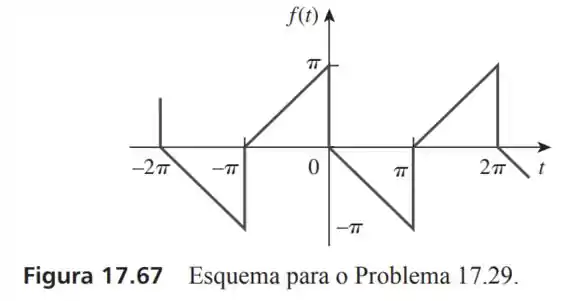
Passo 1
Para a onda descrita no enunciado nós podemos ver que a parte de cima é simétrica com a parte de baixo, sendo portanto uma simetria de meia onda e para expanão em Fourier essa série nos dá:
Além de que podemos pegar somente a meia parte dessa função para construir nossa série de Fourier, pois a área será a mesma. Então vamos pegar a parte:
O período que vamos utilizar é:
Portanto :
Passo 2
O valor de será:
Para a integral por partes aí temos:
Então:
Portanto:
Só que como para qualquer inteiro nós teremos:
Para par:
Para impar:
A última consideração para simetria de meia onda é que só devemos considerar os ímpar. Caso seja diferente de zero.
Passo 3
Agora para encontrar :
Onde a integral por partes:
Portanto:
Então:
Só que para qualquer n inteiro então temos:
Para ímpar temos:
Então temos duas formas de escrever essa série:
Onde
Com esses valores temos o seguinte gráfico:
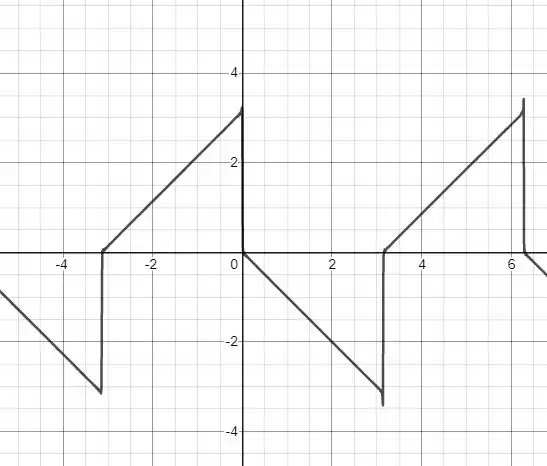
Ou simplesmente:
O gráfico no Desmos está nesse link aqui:
https://www.desmos.com/calculator/x64ripqofu