Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 4.Problemas - Ex. 44
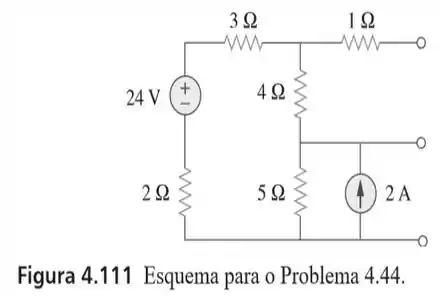
44. Para o circuito da figura , obtenha o equivalente de , conforme visto dos terminais:
(a)
(b)
Passo 1
a) Bom! A primeira coisa que temos que fazer, e encontrar a resistência equivalente nos terminais do resistor . Por isso, vamos ter que redesenhar esse circuito, excluindo as fontes de tensão e de corrente que nele estão presentes.
E aqui está nossa figura:
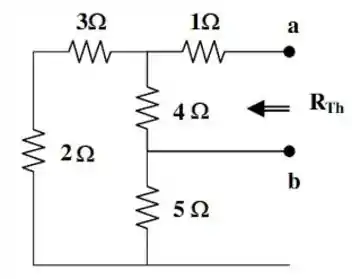
As resistências , e estão em série. E o resultado dessa associação em série, está em paralelo com a resistência de . Baseado nessa figura e na nossa dedução, podemos ver que a resistência de , , é dada por:
Passo 2
Em seguida, o próximo passo é obter a tensão de , .
Por isso, vamos dar uma redesenhada nesse circuito, a fim de vermos o que podemos fazer.
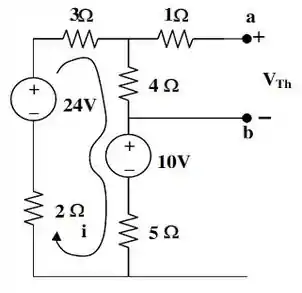
Nenhum corrente vai estar circulando no resistor de . Sendo assim, vamos usar a análise da malha, para determinar a corrente que está circulando nela. Bora lá!
E o valor da tensão entre e , que é a nossa tensão de , vai ser igual a:
Passo 3
b) Para essa letra, vamos tomar o mesmo procedimento do realizado na letra (a). Primeiro, temos que encontrar a resistência de , , retirando do circuito quaisquer fontes de tensão e corrente:
Desse jeito...
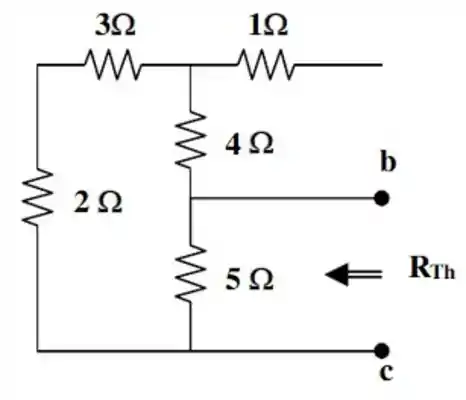
As resistências , e estão em série. E o resultado dessa associação em série, está em paralelo com a resistência de . Não iremos considerar a resistência de em nossa análise, porque ela faz contato direto com o terminal .
Baseado na figura acima e na nossa dedução, podemos ver que a resistência de , , é dada por:
Passo 4
Para obter a tensão de , , bora utilizar a análise nodal. E pra isso, façamos o esboço desse circuito, indicando os nós e as fontes de corente, que nele estão presentes:
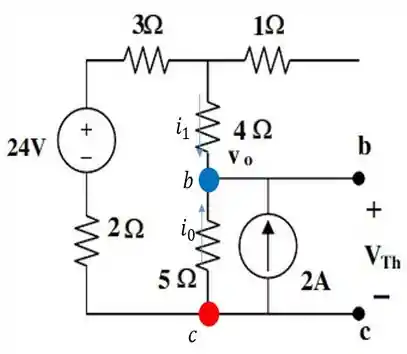
Podemos ver, utilizando a lei das correntes de para o nó , que:
O nó é o nosso Terra, com tensão igual a . Sendo assim, as correntes são dadas em função das tensões nodais, por:
E substituindo essas relações, na fórmula da ), obtemos que:
A tensão de , é dada pela diferença entre as tensões em e . Só que isso aí, é o nosso , né não!?
Conseguimos, desse modo, que:
Resposta
a)
b)