Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 4.Problemas - Ex. 43
43. Determine o equivalente de a partir dos terminais e do circuito mostrado na figura
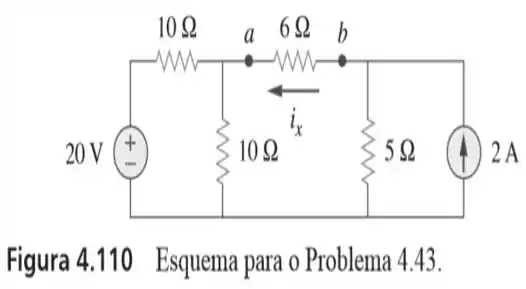
Passo 1
Bom! A primeira coisa que temos que fazer, e encontrar a resistência equivalente nos terminais do resistor . Por isso, vamos ter que redesenhar esse circuito, excluindo as fontes de tensão e de corrente que nele estão presentes, bem como tirando aquela resistência de .
E aqui está nossa figura:
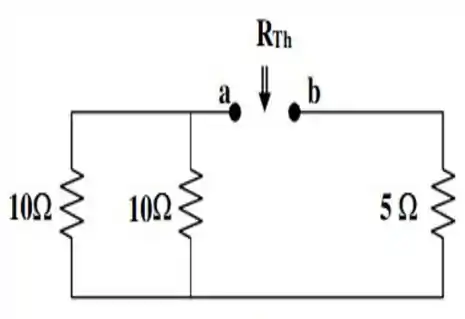
Baseado nessa figura, podemos ver que a resistência de , , é dada por:
Passo 2
Em seguida, o próximo passo é obter a tensão de , .
Por isso, vamos dar uma redesenhada nesse circuito, a fim de fazermos a análise das tensões nos nós...
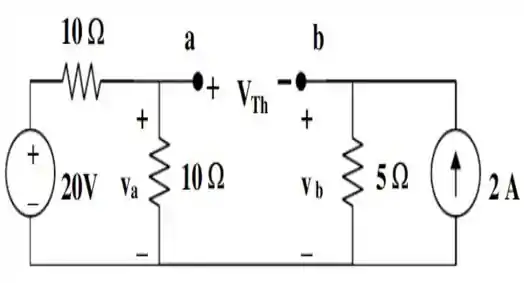
Por essa figura, podemos ver que a corrente de , já que o circuito foi aberto, acabará passando pelo resistor de . Sendo assim, a nossa tensão é dada por:
E usando a divisão de tensão, temos que o valor de é igual a:
A tensão de , é obtida, como podemos ver na figura anterior; pela seguinte relação:
E pronto! Missão cumprida! Obtemos o equivalente de !