Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 4.Problemas - Ex. 69
69- Determine a potência máxima transferida para o resistor no circuito da Figura
Passo 1
Vamos substituir a resistência por uma fonte de corrente de para conseguirmos encontrar a resistência de Thévenin. A fonte de tensão nos daria uma noção errada do circuito, uma vez que passaria sim uma corrente do nó para o nó .
Onde podemos fazer uma resistência equivalente entre os resistores de e de pois eles estão sob influência da mesma tensão
Logo:
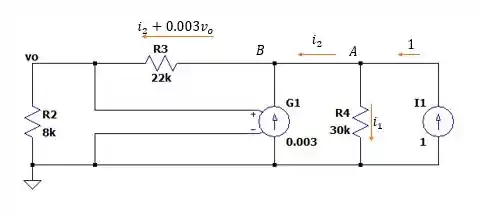
Pela somatória das correntes nesse circuito nós temos:
E temos tensões iguais a:
Então pela segunda equação.
Porém aí que vem a sacada:
A fonte de corrente faz com que surja corrente na linha (onde não normalmente não passaria nenhuma corrente). De tal forma que:
Substituindo o valor das correntes na primeira equação de todas nós temos:
Dessa forma:
Dessa forma a resistência de Thévenin será:
Passo 2
Aí que vem a questão, pois o circuito ativo fez com que a resistência de Thévenin equivalente fosse negativa, aí vamos substituir isso na fórmula da potência máxima.
Ou simplesmente ser escrita como:
Onde normalmente se considera para , mas caso a resistência de Thévenin seja negativa escrevemos da segunda forma, pois não há resistência negativa no mercado.
Isso nos dá uma potência infinita, uma vez que sempre será positivo. Então ‘’teoricamente’’ a fonte pode fornecer a potência que for que o circuito irá (retribuir a energia fornecida). Logo: