Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 4.Problemas - Ex. 61
61- Obtenha os circuitos equivalentes de Thévenin e de Norton nos terminais do circuito da Figura .
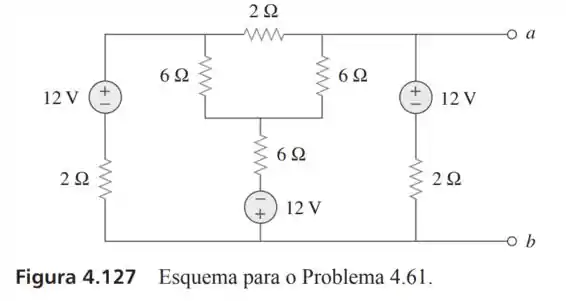
Passo 1
Vamos retirar as fontes independentes de tensão e calcular a resistência equivalente de Thévenin.
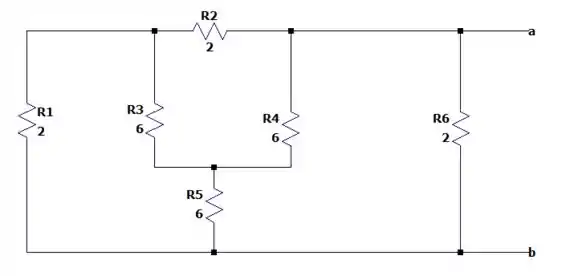
Note que os resistores de formam uma associação em estrela
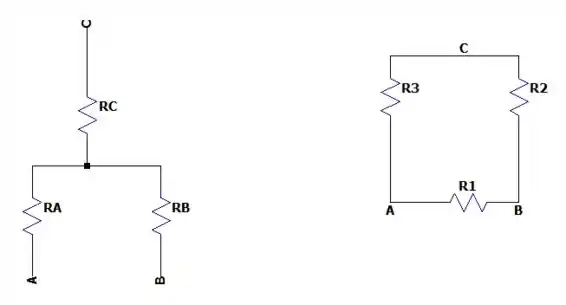
Poderíamos ver os resistores de e de como delta sem problemas também. Fazendo essas transformações vemos que os três resistores viram resistores de:
E o circuito fica da seguinte maneira:
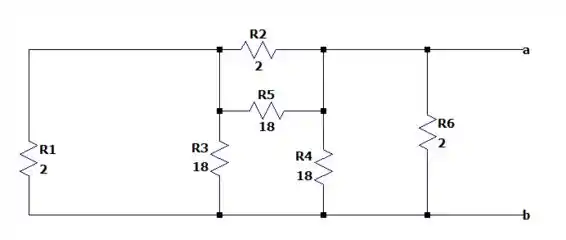
Fazendo a resistência equivalente entre os resistores de e de temos:
Dessa forma temos mais dois conjuntos de resistores de e de em paralelo. O que nos dá o circuto equivalente igual a:
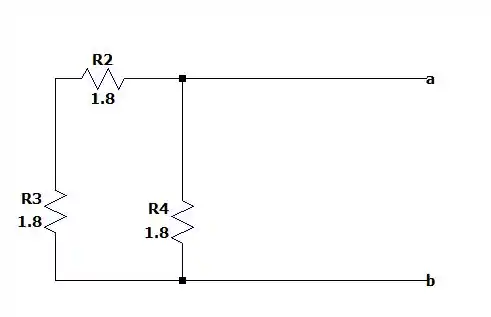
E dessa forma temos os resitores e em série e o equivalente deles em paralelo com nos dando finalmente uma resistência de Thévenin igual a:
Passo 2
Agora vamos resolver o circuito equivalente de uma outra forma, vamos transformar os resistores de e na malha do meio em um circuito estrela, da seguinte forma.
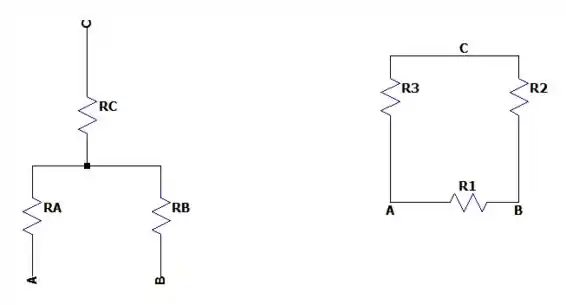
Ou seja o seguinte circuito que é assimficará:
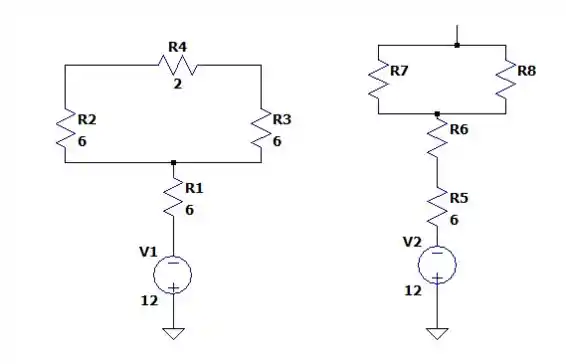
Ou seja:
Deixando o circuito da seguinte forma:
Passo 3
Vamos descobrir pela soma das tensões nas duas malhas
Pela simetria das duas malhas conseguimos ver que:
E pela análise das tensões na malha esquerda vemos que:
Lembrando que só interfere na corrente pelo resistor , a fonte não entra duas vezes na conta. Na conta já consideramos com sinal invertido.
Dessa forma será:
Como está aterrado então
Dessa forma a corrente de Norton será: