Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 13.Problemas - Ex. 4
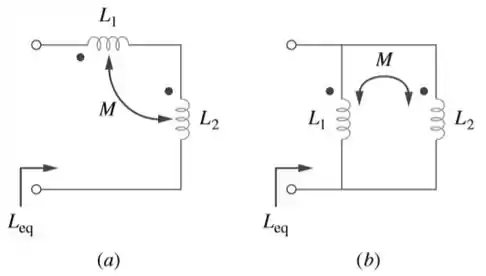
- Para as bobinas acopladas na Figura 13.74a, demonstre que
- Para as bobinas acopladas na Figura 13.74b demonstre que
Passo 1
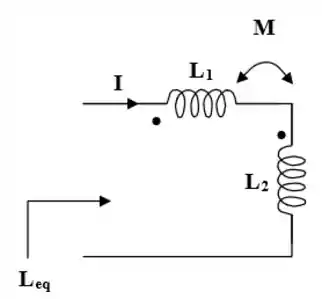
All right! Vamo que vamo! Primeiro vamos observar que para a conexão em série mostrada na figura abaixo a corrente I entra em cada bobina a partir do seu terminal pontilhado. Portanto, as tensões induzidas mutuamente têm o mesmo sinal que as tensões auto-induzidas. Portanto,
Passo 2
O item a) foi tranquilo. O item b) n vai ser diferente! Temos esse circuito:
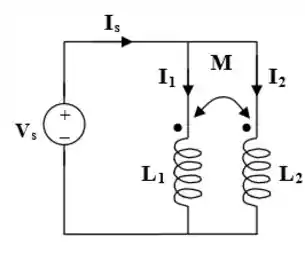
Aplicando LKV para o circuito, temos que:
Ou,
Passo 3
Portanto, para essa matriz, temos:
Portanto para achar a corrente total, vamo somar as duas com os valores dos detlas já achados!
Passo 4
Portanto para finalizar voltamos para a formula da impedância equivalente!
Resposta
Exercícios de Livros Relacionados
As autoindutâncias de dois enrolamentos acoplados magneticamente são L 1 = 180μ HeL 2 = 500μ H . O meio de acoplamento é não magnético. Se o enrolamento 1 tiver 300 espirais e o enrolamento 2,500 espi
Dois enrolamentos acoplados magneticamente são enrolados em um núcleo não magnético.A autoindutância do enrolamento 1 é 288 mH, a indutância mútua é 90 mH, o coeficiente de acoplamento é 0,75 e a estr