Calcule a transformada de Laplace do trem de impulsos unitários da figura.
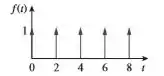
Passo 1
Poxa, sabemos que a transformada de um impulso unitário em (delta de Dirac ) representado aqui figura...

É...
No nosso caso, não temos apenas um impulso e sim um trem de impulsos a cada .
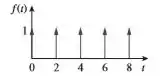
Isso significa dizer que a nossa função delta é periódica e de período , já que a cada ele se repete :
Ora, a transformada de Laplace de uma função periódica de período pode ser calculada da seguinte maneira:
Então, no nosso caso...