Para o circuito com amplificador operacional da Figura 7.138, seja = 10 k, = 20 k, C = 20 F e v(0) = 1 V. Determine .
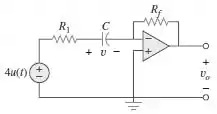
Passo 1
Para resolver este circuito, vamos utilizar a análise por tensões de nó, portanto o circuito fica:
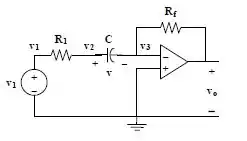
Passo 2
Agora que já dividimos o circuito em nós vamos obter as equações para cada nó.
Para o nó 2:
Para o nó 3:
Por conta do amplificador operacional sabemos que .
Observe também que
Logo,
Simplificando a eq do nó 2, temos:
Ou,
Passo 3
O próximo passa é resolver esta equação diferencial. Sabemos que a solução dela é dada por:
De modo que, a questão nos oferece
Agora só substituir na equação, sabemos que
Portanto,
Passo 4
Lembre-se que a questão nos pede é . Mas já sabemos do nó 3 que:
Simplificando,
Como,
Então
Ou,