No circuito com amplificador operacional da Figura , determine para . Seja .
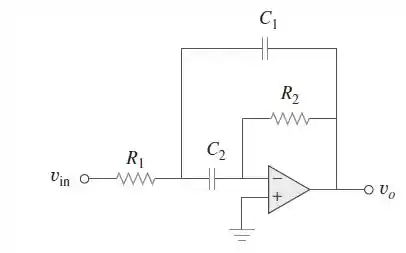
Passo 1
Galera, vamos assumir aqui que o nosso amp-op é ideal, beleza? Assim, podemos assumir o seguinte:
Onde:
- : é a corrente no terminal não-inversor;
- é a corrente no terminal inversor;
- : é a tensão no nó não-inversor;
- : é a tensão no nó inversor.
Como os resistores e capacitores são iguais, vamos adotar a seguinte nomenclatura:
Passo 2
Bom, pessoal, do nosso circuito, temos que:
Seja o nó 1 localizado entre o terminal positivo do primeiro capacitor e o primeiro resistor. Aplicando a lei dos nós para ele, temos:
Aplicando a lei dos nós para o nó inversor do amp-op, temos:
Integrando dos dois lados da equação, temos:
Passo 3
Substituindo a equação e em :
Dividindo por e substituindo :
Derivando essa equação toda em relação a , temos:
A equação característica pode ser expressa como:
As raízes dessa equação são iguais a:
Nos levando a ter a seguinte equação para :
Passo 4
Quando , temos as seguintes condições iniciais:
Agora, quando , e precisamos descobrir . Assim, substituindo em :
Quando , estamos em regime permanente. Os dois capacitores atuam como circuito aberto, logo não há fonte conectada a .
Passo 5
Substituindo os valores encontrados em e na equação para .
Derivando e substituindo , e em em ,
Por fim, substituindo e na equação :
Resposta
O valor da tensão é igual a: