Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 6.Problemas - Ex. 49
Determine a indutância equivalente do circuito da figura 6.72. Suponha que todos os indutores sejam de .
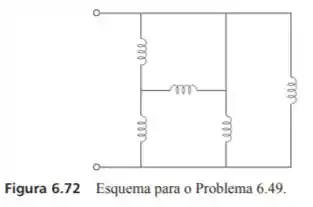
Passo 1
Para calcularmos a indutância equivalente podemos proceder da mesma forma que iríamos proceder caso fossem resistores. Antes de tudo, porém, vamos nomear os nossos nós para facilitar a visualização de quem tá em série e quem tá em paralelo, dessa forma, teremos
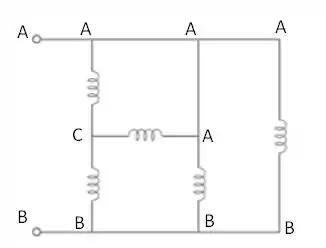
Ainda assim, o circuito fica complicado de desenhar e para facilitar nossa vida vamos reescrevê-lo de uma forma mais simpática sinalizando os pontos marcados
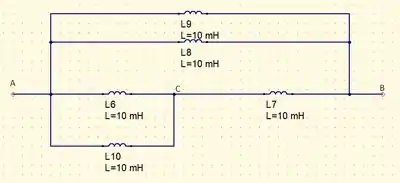
Agora sim fica muito mais evidente quem é que está em série e quem está em paralelo com quem. Assim como para resistores de mesmo valor podemos calcular a resistência equivalente em paralelo pegando o valor da resistência e dividindo pelo número de resistores podemos fazer também para os indutores, então, efetuando a operação para os indutores em paralelo vamos ter o seguinte circuito simplificado
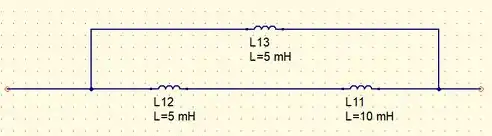
Agora, para os indutores e podemos fazer a associação em série que é a soma de ambos e vamos obter o circuito simplificado
Por fim, para os indutores em paralelo com valores diferentes, vamos ter
Como, nesse caso, só temos 2 indutores a indutância equivalente vai ser dada pela multiplicação sobre a soma. Assim, obtemos