Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 10.Problemas - Ex. 89
O circuito com na figura é chamado . Demonstre que a impedância de entrada é dada por
Onde
Passo 1
Pessoal, para um amplificador operacional ideal, a tensão no terminal inversor é igual a tensão no terminal não inversor. O circuito abaixo é o mesmo do enunciado, mas com nome nos nós.
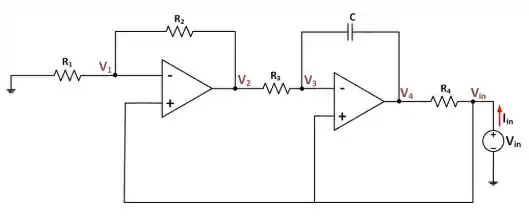
Portanto, podemos escrever que:
A corrente pode ser calculada através de:
Passo 2
Aplicando a lei das correntes de Kirchhoff e a lei de Ohm no nó , temos:
Aplicando a lei das correntes e a lei de Ohm no nó 1:
Passo 3
Substituindo a equação na equação , temos que:
Substituindo a equação na equação ,
Passo 4
Da equação , podemos inferir a impedância de entrada!
Pronto, devidamente demonstrado! 😊
Resposta
Ei, a resposta está no passo a passo :)