Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 13.Problemas - Ex. 71

No circuito com autotransformador da Figura 13.134 , demonstre que

Z e n t = 1 + N 1 N 2 2 Z L

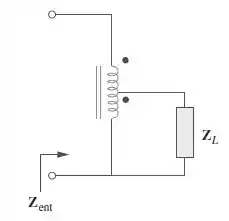
Passo 1

Partiu demonstrar essa equação aí! Podemos escrever a impedância de entrada da seguinte forma:

Z e n t = V 1 / I 1 … ( 1 )

A tensão no secundário do transformador pode ser expressa por:

V 2 = I 2 Z L … ( 2 )

Bom, vamos escrever agora a relação entre as tensões e as correntes no autotransformador:

V 1 V 2 = I 2 I 1 = N 1 + N 2 N 2

I 2 = I 1 N 1 + N 2 N 2 … ( 3 )

Passo 2

Reorganizando a expressão acima, evidenciando V 1 :

V 1 = V 2 I 2 I 1 … ( 4 )

Substituindo a equação ( 2 ) em ( 4 ) , temos:

V 1 = I 2 Z L I 2 I 1

V 1 = Z L I 2 2 I 1

Substituindo a equação ( 3 ) na equação anterior:

V 1 = Z L I 1 I 1 N 1 + N 2 N 2 2

V 1 = Z L I 1 I 1 2 N 1 + N 2 N 2 2

V 1 = Z L I 1 1 + N 1 N 2 2

V 1 I 1 = Z L 1 + N 1 N 2 2

Z e n t = 1 + N 1 N 2 2 Z L

Pronto! Conforme queríamos demonstrar! 😊

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

No circuito da Figura 13.132 , Z L é ajustada até a máxima potência media ser liberada para Z L . Determinar Z L e a máxima potência média transferida para ela. Considere N 1 = 600 espiras e N 2 = 200
No circuito do transformador ideal da Figura 13.133 , determine a potência média liberada para a carga.
No autotransformador ideal da Figura 13.131 , calcule I 1 ,I 2 e I 0 . Determine a potência média liberada para a carga.
Considere o transformador trifásico mostrado na Figura 13.136 . O primário é alimentado por uma fonte trifásica com tensão de linha de 2,4k VR M S , enquanto o secundario alimenta uma carga equilibrad
Considere a Figura 13.138 e elabore um problema para ajudar outras estudantes a entender melhor como funciona um transformador trifásico e a conexão estrela-triângulo.