Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 17.Problemas - Ex. 48

Para o circuito da figura

i t = 20 + 16 cos ⁡ 10 t + 45 ° + 12 cos ⁡ 20 t - 60 °   m A

  1. Determine v t
  2. Calcule a potência média dissipada no resistor.

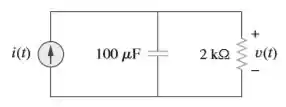
Passo 1

Para calcular a tensão de corrente contínua usando a corrente DC i = 20 m A , consideremos o capacitor aberto e pela lei de Ohm...

v = R ⋅ i = 2 ⋅ 10 3 ⋅ 20 ⋅ 10 - 3 =

40 V

Passo 2

Agora, para calcular as demais tensões, consideremos as impedâncias:

Z r = 2 ⋅ 10 3

Z c = 1 j ω C  

Onde ω é a frequência angular dos cossenos e que pode ser 10 e 20 . No geral, podemos falar que ω n = 10 n (onde n é 1 ou 2 ), dessa forma:

Z c = 1 j 10 n ⋅ 100 ⋅ 10 - 6

Como 1 j = - j e 10 ⋅ 100 ⋅ 10 - 6 = 10 - 3 ...

Z c = - j 1 n ⋅ 10 3

Logo, a impedância total no nosso caso, será o paralelo entre Z r Z c :

Z t = Z r / / Z c

Ou seja

Z t = 2 ⋅ 10 3 ⋅ - j 1 n ⋅ 10 3 2 ⋅ 10 3 - j 1 n ⋅ 10 3     →

Simplificando...

Z t = - 2 j n ⋅ 10 6 2 - j n ⋅ 10 3     →

Z t = - 2 j n 2 n - j n 10 3     →

Onde concluímos que...

Z t = - 2 j 2 n - j 10 3

Passo 3

Pela Lei de Ohm então sabemos que...

V n = Z t ⋅ I n =

- 2 j 2 n - j 10 3 ⋅ I n

Perceba que tem n em todo mundo, pois depende da frequência. A corrente no domínio da frequência, por exemplo, se estivermos falando do I 1 é o cara que depende do cosseno de n = 1 :

16 cos ⁡ 10 t + 45 °

I 1 = 16 ∠ 45 ° ⋅ 10 - 3  

Saca?

Vamos primeiro então calcular V 1 fazendo n = 1 :

V 1 = - 2 j 2 ⋅ 1 - j 10 3 ⋅ I 1   →

V 1 = - 2 j ⋅ 16 ∠ 45 ° 2 - j 10 3 ⋅ 10 - 3     →

Passando todo mundo para polar...

V 1 = 2 ∠ - 90 ° ⋅ 16 ∠ 45 ° 2,236 ∠ - 26,56 °   →

V 1 = 32 ∠ - 45 ° 2,236 ∠ - 26,56 °   →

V 1 = 14,311 ∠ - 18,44 °

Agora para n = 2 ...

V 2 = - 2 j 2 ⋅ 2 - j 10 3 ⋅ I 2   →

Onde o I 2 dessa vez é...

12 cos ⁡ 20 t - 60 °

I 2 = 12 ∠ - 60 ° ⋅ 10 - 3  

Então...

V 2 = - 2 j ⋅ 12 ∠ - 60 ° 4 - j 10 3 ⋅ 10 - 3     →

V 2 = 2 ∠ - 90 ° ⋅ 12 ∠ - 60 ° 4,123 ∠ - 14 , 03 °   →

V 2 = 5,567 ∠ - 135,97 °

Passo 4

Beleza! Agora podemos calcular a potência média:

p = V d c I d c + 1 2 ∑ n = 1 ∞ V n I n cos ⁡ Θ n - Φ n

Onde V d c é a tensão de corrente contínua obtida lá no passo 1 :

V d c = 40 V = 40

I d c = 20 ⋅ 10 - 3  

Enquanto que os V ’s que depende de n tem esse resulmão dos passos anteriores:

P a r a   n = 1         →           V 1 = 14,311 ⋅ 10 3 ∠ Θ 1               o n d e           Θ 1 = - 18,44 ° I 1 = 16 ⋅ 10 - 3 ∠ Φ 1                 o n d e                 Φ 1 = 45 °

P a r a   n = 2         →           V 2 = 5,567 ⋅ 10 3 ∠ Θ 1               o n d e           Θ 1 = - 135,97 ° I 2 = 12 ⋅ 10 - 3 ∠ Φ 1                 o n d e                 Φ 1 = - 60 °

Logo...

p = V d c I d c + 1 2 ∑ n = 1 ∞ V n I n cos ⁡ Θ n - Φ n     →

p = 40 ⋅ 20 ⋅ 10 - 3 + 1 2 V 1 I 1 cos ⁡ Θ 1 - Φ 1 + V 2 I 2 cos ⁡ Θ 2 - Φ 2     →

p = 40 ⋅ 20 ⋅ 10 - 3 + 1 2 14,311 ⋅ 16 ⋅ 10 - 3 cos ⁡ - 18,44 ° - 45 ° + 5,567 ⋅ 12 ⋅ 10 - 3 cos ⁡ - 135,97 ° + 60 °     →

p = 800 + 114,488 cos ⁡ - 63,43 ° + 33,402 cos ⁡ - 75,97 ° ⋅ 10 - 3   →

p = 800 + 114,488 cos ⁡ - 63,43 ° + 33,402 cos ⁡ - 75,97 ° ⋅ 10 - 3   →

p = 800,1 m W

Resposta

p = 800,1 m W

Ver Outros Exercícios desse livro