Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 19.Problemas - Ex. 69
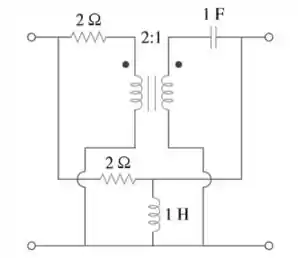
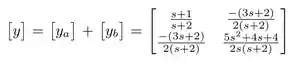O circuito da figura pode ser considerado dois circuitos de duas portas ligados em paralelo. Obtenha os parâmetros em função de .
Passo 1
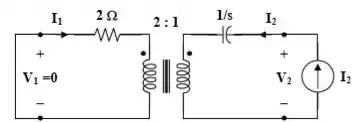
Vamos primeiro determinar os parâmetros .
Para obter fazemos, dado que :
Então,
E a corrente é:
Passo 2
Para obter temos:
Para a tensão:
Para a corrente:
Logo, a matriz será:
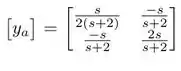
Passo 3
Na outra parte do circuito obteremos a matriz :
Para :
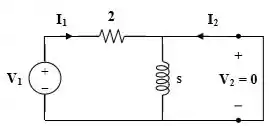
Para a tensão:
Para a corrente:
Passo 4
Para obter temos:
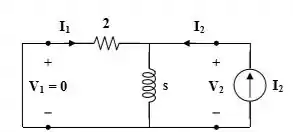
Para a tensão:
Para a corrente:
Então, montamos a matriz:
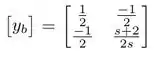
Passo 5
Por fim, somamos as duas matrizes:
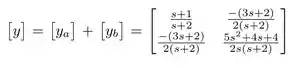
Resposta
