Enunciado
Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 2.Problemas - Ex. 17
Considere o circuito mostrado na Figura P2.17.
a) Determine usando as leis de Kirchhoff e a lei de Ohm.
b) Teste a solução para , verificando que a potência total fornecida é igual à potência total absorvida.
Passo 1
Iae, meus queridos! Td certinho??
Partiu para mais uma questão muito bacana de circuitos.
Primeiro vamos desenhar o circuito que vamos trabalhar.
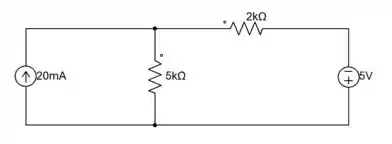
Letra a) Para resolver este circuito, vamos usar o método de analise de malhas, que é o que nos foi solicitado no enunciado.
Para a malha 1, temos:
Para a malha 2, temos:
Assim, temos:
A partir da primeira equação, vemos que Substituindo na segunda equação, temos.
Aplicando a lei de ohm em :
Passo 2
Para a letra b), vamos calcular a potência absorvida pelo resistor de 5k e a potência que é fornecida a ele.
Para calcular a potência absorvida, utilizamos a equação:
Já a potência fornecia será.
Provamos que a potência fornecia é igual a potência absorvida em .
Tranquilo, né?
Resposta
A)
B)