Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - James W. Nilsson, Circuitos Elétricos- Ed: 10º - Capítulo 2.Problemas - Ex. 39

Para o circuito mostrado na Figura 2.24, R1 = 40 kV, R2 = 60 kV, RC = 750 V, RE = 120 V, VCC = 10 V, V0 = 600 mV e β = 49. Calcule iB, iC, iE, v3d, vbd, i2, i1, vab, iCC e v13. (Observação: na notação das tensões variáveis com dois índices, o primeiro é positivo em relação ao segundo. Veja Figura P2.39.)

Passo 1

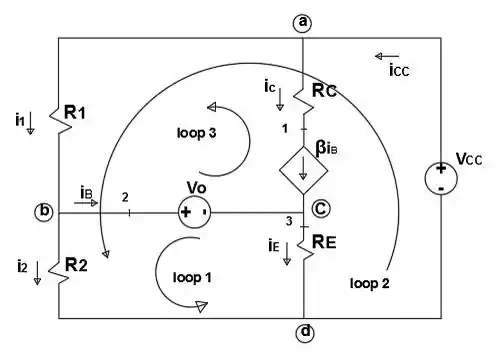
Beleza?! Primeira coisa que você vai fazer depois de pegar seu lápis e seu papel é claro, é da uma analisada cuidadosa na nossa figura. Temos 3 Loops e iremos equacioná-los para assim obtermos os valores que queremos.

Para o Loop 1:

- v 0 + i 2 R 2 - i E R E = 0

- 0.6 + i 2 60000 - i E 120 = 0

60000 i 2 - 120 i E - 0.6 = 0

60000 i 2 - 120 i B 50 - 0.6 = 0

60000 i 2 - 6000 i B - 0.6 = 0       ( 1 )

Para o Loop 2:

- v c c + i 1 R 1 + i 2 R 2 = 0

- 10 + 40000 i 1 + 0000 i 2 = 0

40000 i 1 + 60000 i 2 - 10 = 0     ( 2 )

Passo 2

Equacionando o nó b:

i 1 - i B - i 2 = 0       ( 3 )

Resolvendo as equações, encontramos

i 1 = 0.208 m A

i 2 = 0.028 m A

i B = 0.18 m A

Agora equacionando o nó 1:

i c - β i B = 0

i c = β i B

i c = 49 ∙ 0.18 ∙ 10 - 3

i c = 8.82 m A

Passo 3

Equacionando o nó a:

i c c - i c - i 1 = 0

i c c - 49 i B - i 1 = 0

i c c = 49 ∙ 0.18 ∙ 10 - 3 - 20.8 ∙ 10 - 3

i c c = 29.62 m A

Novamente equacionando um nó, agora o c:

β i B + i B - i E = 0

49 i B + i B - i E = 0

i E = 50 i B

i B = 50 ∙ 0.18 ∙ 10 - 3

i E = 9 m A

v a b = v a - v b = i 1 R 1

v a b = 0.208 ∙ 10 - 3 ∙ 40000

v a b = 8.32 V

v b d = i 2 ∙ R 2

v b d = 0.028 ∙ 10 - 3 ∙ 60000

v b d = 1.68 V

v 3 d = i E ∙ R E

v 3 d = 9 ∙ 10 - 3 ∙ 120

v 3 d = 1.08 V

Finalmente chegando ao último Loop, ao 3:

- v 0 + v c 1 - i c R c + i 1 R 1 = 0

v c 1 = v 31 = - v 13

v 0 - v 13 - i c R c + i 1 R 1 = 0

0.6 - v 13 - 8.82 ∙ 10 - 3 ∙ 750 + 0.208 ∙ 10 - 3 ∙ 40000 = 0

v 13 = 2.305 V

Resposta

i B = 0.18 m A i c = 8.82 m A

i E = 9 m A

v 3 d = 1.08 V

v b d = 1.68 V

i 2 = 0.028 m A

i 1 = 0.208 m A

v a b = 8.32 V

i c c = 29.62 m A

v 13 = 2.305 V

Exercícios de Livros Relacionados

No circuito da figura 2.75 , determine V_1 e V_2 .
Deduza a Equação 2.25. Sugestão: use as equações (3) e (4) do Exemplo 2.11 para expressar i E como uma função de i B. Resolva a Equação (2) para i 2 e substitua o resultado nas equações (5) e (6). Res
As correntes i a e i b no circuito da Figura P2.26 são 4 A e -2 A, respectivamente. a) Determine i g. b) Determine a potência dissipada em cada resistor. c) Determine vg. d) Mostre que a potência forn
Para o circuito mostrado na Figura P2.36, calcule i ∆ e v σ e (b) mostre que a potência fornecida é igual à potência absorvida.