Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 12.Problemas - Ex. 20
Considere a Figura 12.51 e elabore um problema para ajudar outros estudantes a entender melhor os circuitos conectados em triângulo-triângulo equilibrado.
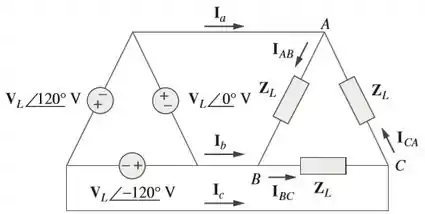
Passo 1
Eita!! O jogo virou hein? Hahaha! Brincadeiras de lado, elaborar questões é uma forma bem eficiente de aprender mais sobre o assunto! Então, mãos na massa! A questão é:
Consulte o circuito na Fig. 12.51. Encontre a linha e as correntes de fase. Suponha que a impedância de carga seja por fase.
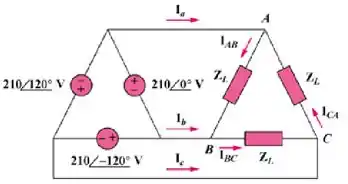
Passo 2
Beleza, vamos lá! Primeiro de tudo é achar o tão falado ! Ele vai nos guiar para acharmos as correntes de fase e posteriormente as correntes de linha!
Portanto,
Passo 3
Agora vamos achar as correntes de linha com base nas correntes de fase!
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
As leituras do medidor para um alternador trifásico ligado em estrela que fornece energia para um motor indicam que as tensões de linha são 330V , as correntes de linha são 8,4A e a potência total de
O método dos dois wattímetros fornece P 1=1200WeP 2=400W para um motor trifásico alimentado por uma linha de 240V . Suponha que a carga do motor esteja conectada em estrela e que ela absorva uma corre
Determinada loja tem três cargas trifásicas equilibradas. As três cargas são:Carga 1: 16k V Ac o mF P = 0,85( a t r a s a d o ) Carga 2: 12k V Ac o mF P = 0,6( a t r a s a d o ) Carga 3: 8 k Wc o mF P
Para o circuito mostrado na Figura 12.74, determine as leituras do wattímetro.
Demonstre que as perdas I2 R serão maiores para um aparelho de 120V que para um de 240V , se ambos tiverem a mesma potência nominal.