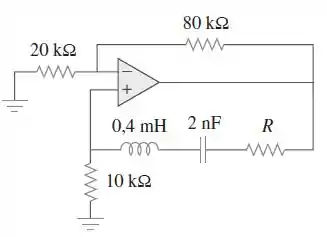
Considere o oscilador da Figura .

1. Determine a frequência de oscilação.
2. Obtenha o valor mínimo de para qual ocorre a oscilação.

Galera, para a letra (a), vamos aplicar o divisor de tensão no terminal não inversor :

deve estar em fase com para satisfazer o segundo critério de Barkhausen. Isso implica em dizer que a razão da equação deveria ser puramente real. Fazendo a parte imaginária ser igual a zero, a frequência de oscilação pode ser encontrada:

Como ,