Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 10.Problemas - Ex. 85
Usando a Figura , elabore um problema para ajudar outros estudantes a entender melhor como realizar a análise com o PSpice ou MultiSim.
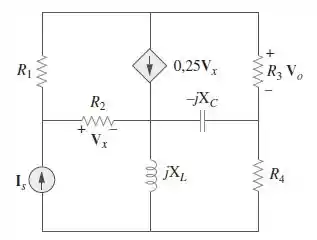
Passo 1
Galera, vamos atribuir valores aos componentes inicialmente.
Assumindo , vamos passar o domínio do tempo os componentes e :
Vamos usar o PSpice para encontrar o valor de no circuito!
Passo 2
Uma vez que as transformações foram feitas, vamos desenhar o circuito no software:
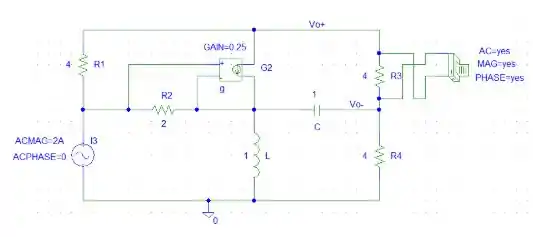
Depois de simular o circuito, o arquivo de saída deverá conter a frequência da fonte e os atributos que escolhemos imprimir, como o módulo da tensão e o ângulo. Assim, conseguimos os valores:
Assim, podemos escrever a resposta como:
Resposta
A tensão é igual a:
Exercícios de Livros Relacionados
O fasor corrente Ib, no circuito da Figura P9.36, é 25 ∠0 º º mA.. a) Determine Ia, Ic e Ig. b) Se v = 1.500 rad/s, determine as expressões para i a(t), i c (t) e i g(t).
Use o método das tensões de nó para determinar a expressão de regime permanente para i o no circuito visto na Figura P9.56, se i g = 5 cos 2.500t A e vg = 20 cos (2.500t + 90º) V.
No circuito da Figura P9.67, suponha que v1 = 20 cos(2.000t - 36,87°) V, v2 = 10 cos(5.000t + 16,26°) V. a) Qual é a técnica de análise de circuitos que deve ser utilizada para determinar a expressão
O amp op no circuito visto na Figura P9.72 é ideal. Determine a expressão de regime permanente para vo(t) quando vg = 2 cos 106t V.
O valor de k no circuito da Figura P9.74 é ajustado de modo que Zab seja puramente resistiva quando v = 4 krad/s. Determine Zab.