Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 2.Problemas - Ex. 48
48. Converta os circuitos da figura de em .
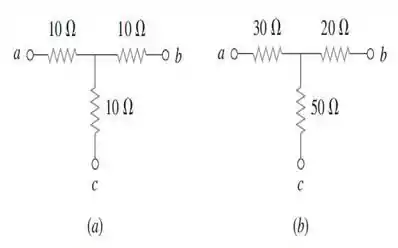
Passo 1
a) Bom! Essa questão é bem mais fácil do que parece. Sabe por quê?
Basta usar as fórmulas já prontas para a conversão de um circuito em . São elas:
Nessa primeira letra , o que nos leva ao seguinte resultado:
Passo 2
b) Já nesse segundo caso, temos que:
Desse jeito, utilizando as fórmulas já conhecidas a seguir:
E substituindos os valores correspondentes:
Obtemos as seguintes respostas:
Resposta
a)
b)
Exercícios de Livros Relacionados
a) O atenuador fixo mostrado na Figura P3.67 é denominado ponte em T. Use uma transformação Y-D para mostrar que Rab = RLse R = R L.b) Mostre que, quando R = RL, a razão vo/vi é igual a 0,50.
a) Se o erro percentual for definido como b) Calcule o erro percentual de vo, usando os valores do Problema 3.69(b).
a)Para o circuito mostrado na Figura P3.69, a ponte está equilibrada quando DR = 0.Mostre que, se DR V Ro, a tensão de saída da ponte é aproximadamenteb) Dados R2 = 1 kV, R3 = 500 V, R4 = 5 kVe vin =
As equações de projeto para o atenuador de ponte em T no circuito da Figura P3.68 são quando R2 tem o valor dado.a) Projete um atenuador fixo, de modo que vi = 3,5vo quando RL = 300 V.b) Suponha que a