Dado um sinal , Determine a taxa de Nyquist e o intervalo de Nyquist para o sinal.
Passo 1
Então galera, vamos lá! Em questões de aplicação, temos sempre que observar isso como se fosse uma questão teórica normal. Tiramos os pontos de cada característica do problema e vamos pra cima pros cálculos!
Passo 2
Primeiro, encontramos a transformada de Fourier de Usamos os resultados do Exemplo 17.2 em conjunto com a propriedade duality. Seja um pulso retangular de altura e largura , como mostrado abaixo. transforma em .
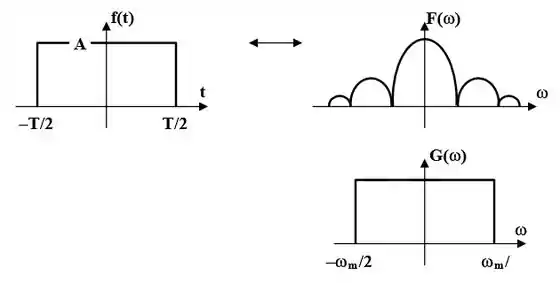
Passo 3
De acordo com a propriedade da dualidade,
Logo,
Onde,
, ou
Passo 4
Para o caso, a frequência superior,
, ou
A frequência de Nyquist,
O intervalo de Nyquist,