Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 17.Problemas - Ex. 65
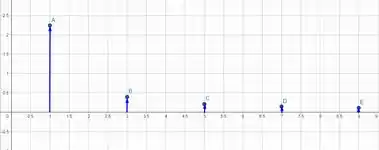
Dado que
Represente graficamente os cinco termos dos espectros de amplitude e de fase para a função.
Passo 1
Dado que a nossa função já veio representada na forma “natural” de Fourier vamos extrair o valor dos nossos coeficientes para facilitar nossas contas
Com esses dados podemos escrever nossos dados para a forma de magnitude utilizando a seguinte transformação
Para facilitar nossa conta montemos a seguinte tabela
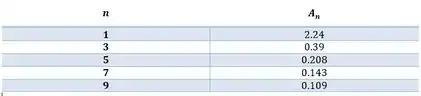
Assim, nosso espectro de amplitude fica sendo
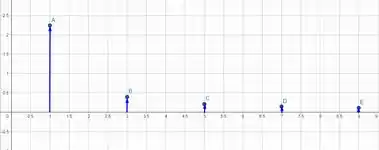
Passo 2
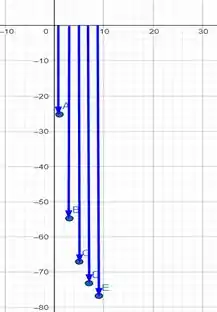
Agora, para o espectro de fase vamos utilizar a seguinte fórmula
Dessa forma, para os variados valores de vamos poder montar a seguinte tabela
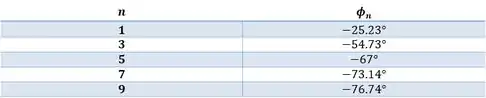
Com isso, nosso espectro de fase fica sendo
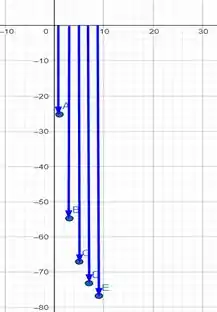
Resposta
