Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 18.Problemas - Ex. 20

  1. Demonstre que um sinal periódico com série de Fourier exponencial

    2. f t = ∑ n = - ∞ ∞ c n e j n ω 0 t

    Apresenta a transformada de Fourier

    F ω = ∑ n = - ∞ ∞ c n δ ( ω - n ω 0 ) ,   o n d e   ω = 2 π / T

  2. Determine a transformada de Fourier do sinal na Figura 18.37 .

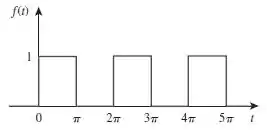
Passo 1

Bom, galerinha, a transformada de Fourier de um sinal periódico produz um espectro de frequência discreto. Portanto, podemos escrever:

F c n = c n δ ω

Assim, nós podemos usar a propriedade de deslocamento de frequência da transformada de Fourier:

F c n e j n ω 0 t = c n δ ( ω - n ω 0 )

Passo 2

Na letra (b) precisamos achar a transformada do sinal dado. O período do sinal é igual a:

T = 2 π ,     ω 0 = 2 π T = 1

Agora podemos determinar o coeficiente de Fourier c n :

c n = 1 T ∫ 0 T f t e - j n ω 0 t d t

c n = 1 2 π ∫ 0 π 1 × e - j n t d t + ∫ π 2 π 0 × e - j n t d t

c n = 1 2 π × 1 - j n e - j n t 0 π

c n = j 2 π n ( e - j n π - 1 )

Passo 3

Além disso, a série de Fourier exponencial para o sinal f ( t ) é:

f t = c 0 + ∑ n = - ∞ ∞ c n e j n t

f t = 1 2 - ∑ n = - ∞ ∞ j n π δ ( ω - n )

A transformada de Fourier do sinal é:

F f t = 1 2 δ ω - ∑ n = - ∞ ∞ j n π δ ( ω - n )

Resposta

  1. F c n e j n ω 0 t = c n δ ( ω - n ω 0 ) ;
  2. F f t = 1 2 δ ω - ∑ n = - ∞ ∞ j n π δ ( ω - n )
Ver Outros Exercícios desse livro