Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 19.Problemas - Ex. 96

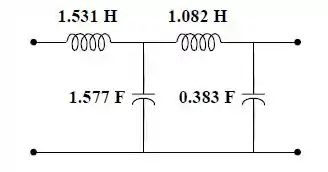
Desenhe um circuito em cascata L C para concretizar um filtro passa-baixa com função de transferência

H ( s ) = 1 s 4 + 2,613 s 3 + 3,414 s 2 + 2,613 s + 1

Passo 1

Galera, um circuito de quarta ordem pode ser feito em cascata L C conforme a figura abaixo:

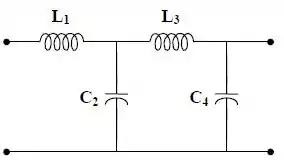
Agora nós temos que determinar os valores das indutâncias e das capacitâncias do circuito!

H s = 1 2,613 s 3 + 2,613 s 1 + s 4 + 3,414 s 2 + 1 2,613 s 3 + 2,613 s

Quando Y L = 1 , apara a função de transferência do filtro passa-baixa é válido o seguinte:

H s = - y 21 1 + y 22

Que indica:

y 21 = - 1 2,613 s 3 + 2,613 s

y 22 = s 4 + 3,414 s 2 + 1 2,613 s 3 + 2,613 s

A expressão simplificada para y 22 é:

y 22 = s C 4 + Y A = 0,383 s + 2,414 s 2 + 1 2,13 s 2 + 2,613 s

Assim, temos que:

C 4 = 0,383   F

Y A = 2,414 s 2 + 1 2,13 s 2 + 2,613 s corresponde a:

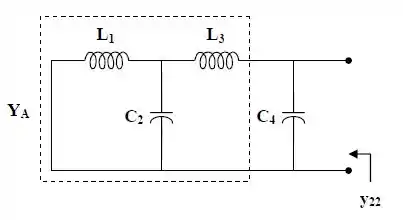
Passo 2

A partir de Y A , podemos escrever a impedância Z A :

Z A = 1 Y A = 2,613 s 3 + 2,613 s 2,414 s 2 + 1

Simplificando a expressão para Z A :

Z A = s L 3 + Z B = 1,082 s + 1,531 s 2,414 s 2 + 1

L 3 = 1,082   H

Z B = 1,531 s 2,414 s 2 + 1 corresponde a:

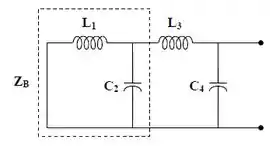
Passo 3

A partir de Z B , podemos escrever a admitância Y B :

Y B = 1 Z B = 1,577 s + 1 1,531 s

Simplificando a expressão para Y B :

Y B = s C 2 + 1 s L 1 = 1,577 s + 1 1,531 s

L 1 = 1 , 531   H

C 2 = 1,577   F

Assim, o circuitp é igual a:

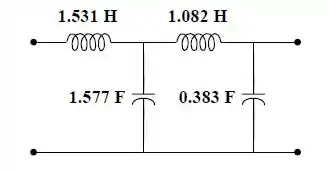
Resposta

Ver Outros Exercícios desse livro