Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 19.Problemas - Ex. 97

Sintetize a função de transferência

H s = V 0 V s = s 3 s 3 + 6 s 2 + 12 s + 24

Passo 1

Pessoal, a função de transferência pode ser reescrita como

H s = s 3 s 3 + 6 s 2 + 12 s + 24 = s 3 s 3 + 12 s 1 + 6 s 2 + 24 s 3 + 12 s

Logo,

y 22 = 6 s 2 + 24 s 3 + 12 s = 1 s C 2 + Z A

Onde Z A corresponde a:

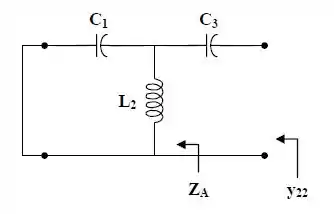
Passo 2

Podemos obter C 3 e Z A através das frações parciais:

y 22 = 6 s 2 + 24 s s 2 + 12 = A s + B s + C s 2 + 12

6 s 2 + 24 = A s 2 + 12 + B s 2 + C s

Aqui temos:

12 A = 24 → A = 2

C = 0

A + B = 6   →     B = 4

Assim,

6 s 2 + 24 s s 2 + 12 = 2 s + 4 s s 2 + 12

Agora comparando,

1 s C 2 + Z A = 2 s + 4 s s 2 + 12

Podemos concluir que

C 3 = 1 2 F

Z A = 4 s s 2 + 12

Passo 3

Nós sabemos que:

1 Z A = s C 1 + 1 s L 2 = s 2 + 12 4 s = 1 4 s + 3 s

Assim, podemos inferir que:

L 2 = 1 3   H

C 1 = 1 4 F

Resposta

C 1 = 1 2 F

L 2 = 1 3   H

C 3 = 1 4   F

Ver Outros Exercícios desse livro