Determine para o amplificador mostrado na figura. Suponha que .
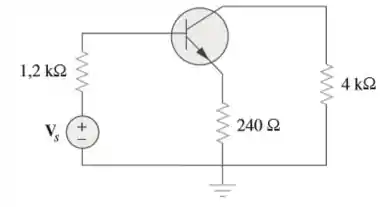
Passo 1
Vamos começar desenhando o circuito equivalente:
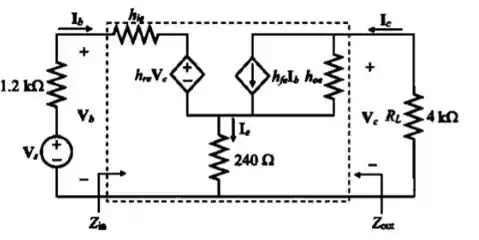
Passo 2
Usando a lei das correntes de Kirchhoff temos:
Agora, usando a lei das tensões de Kirchhoff no lado esquerdo, temos:
E aplicando a lei das correntes de Kirchhoff no nó :
Passo 3
A tensão de saída é:
Substituindo por na equação (3), temos:
Da equação (4), e substituindo o valor encontrado na equação (3) chegamos em :
Passo 4
Agora, queremos achar e para isso substituímos os valores de e na equação 2, chegando em:
Passo 5
Para a impedância interna vamos substituir o valor de na equação 2.
Em seguida, substituímos por em
Chegando em:
Passo 6
Para obter usamos uma fonte de como mostra a figura:
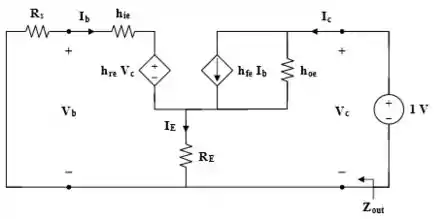
Aplicando a lei de Kirchhoff das tensões do lado esquerdo:
Aplicando a lei de Kirchhoff das correntes no nó :
Passo 7
Substituindo esse resultado do Passo 6 e colocando na equação (5) chegamos no que queremos: