Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 14.Problemas - Ex. 21

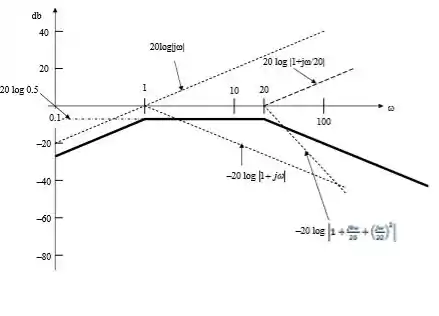
Esboce o gráfico de Bode de amplitude para

H s = 10 s s + 20 s + 1 s 2 + 60 s + 400 ,         s = j ω

Passo 1

Pois bem, vamos começar esse problema, substituindo s por j ω ...

H j ω = 10 j ω j ω + 20 j ω + 1 j ω 2 + 60 j ω + 400

Agora, a gente tem que arrumar essa equação de forma que possamos comparar com essa tabela aqui:

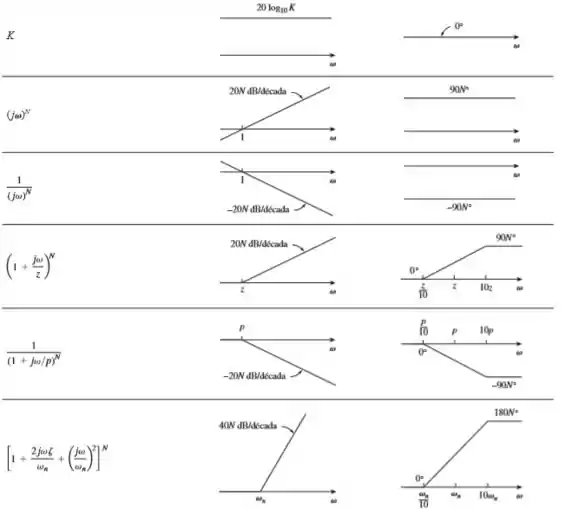
Vamos nessa?

Passo 2

Bem, nesse termo quadrático, precisamos dividir todo mundo por 400 para ficarmos 1 na soma e ganhar ω n , saca? Mas se você dividir por 400 , você tem que multiplicar por 400 para não alterar a equação dessa forma aqui...

H j ω = 10 j ω j ω + 20 400 j ω + 1 j ω 2 400 + 60 j ω 400 + 400 400

Bem, 400 é 20 2 , então...

H j ω = 10 j ω j ω + 20 400 j ω + 1 j ω 20 2 + 60 j ω 400 + 400 400

Veja então que ω n nesse caso é 20 .

Passo 3

Agora vamos fazer algo semelhante com esse j ω + 20 ...

H j ω = 10 ⋅ 20 j ω j ω 20 + 20 20 400 j ω + 1 j ω 2 400 + 60 j ω 400 + 400 400   →

H j ω = 200 j ω j ω 20 + 1 400 j ω + 1 j ω 2 400 + 60 j ω 400 + 400 400   →

H j ω = 1 2 j ω j ω 20 + 1 j ω + 1 j ω 2 400 + 60 j ω 400 + 400 400   →

Finalmente a gente pode agora aplicar o 20 log ⁡   em todo mundo...

Passo 4

20 log ⁡ H j ω = 20 log ⁡ j ω 2 j ω 20 + 1 j ω + 1 j ω 20 2 + 60 j ω 400 + 1   →

De acordo com propriedades do Log...

20 log ⁡ H j ω = 20 log ⁡ j ω 2 j ω 20 + 1 - 20 log ⁡ j ω + 1 j ω 20 2 + 60 j ω 400 + 1   →

20 log ⁡ H j ω = 20 log ⁡ j ω + 20 log ⁡ 0.5 + 20 log ⁡ j ω 20 + 1 - 20 log ⁡ j ω + 1 - 20 log ⁡ j ω 20 2 + 60 j ω 400 + 1   →

Podemos desenhar isso aí agora observando a tabela do passo 1:

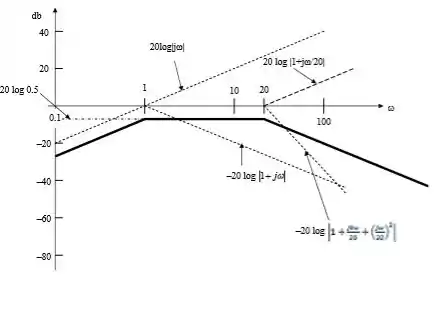
Viu só !

Resposta

Ver Outros Exercícios desse livro