Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 6.Problemas - Ex. 55

Determine a em cada um dos circuitos da figura 6.77.

Passo 1

Devemos lembrar que a regra que vale para os indutores é igual a regra que vale para os resistores ou seja

Onde representa uma associação em série e associação em paralelo. Para o primeiro circuito vamos ter ambas as formas de associações começando com os que estão em paralelo (de forma mais evidente)

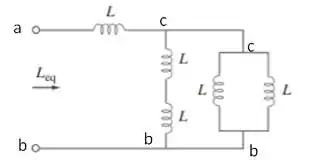
Entre os potenciais temos as associações em série e em paralelo e que resultarão em

Esses dois vão estar associados em paralelo e resultarão em

Por fim, para concluir o exercício basta somarmos esse resultado com pois eles estão em série agora, então, teremos

Passo 2

Para o segundo exemplo, analisando cada um dos triângulos que aparecem no nosso circuito vamos perceber que individualmente os dois indutores que aparecem em cada triângulo estão em paralelo entre si, assim, seu equivalente é dado por

Esses, por sua vez estarão em série um com outro e dessa forma obtemos

Esse indutor estará em paralelo com o último indutor e, por fim, vamos obter

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

O pulso triangular de corrente mostrado na Figura P6.2 é aplicado a um indutor de 500 mH. a) Escreva as expressões que descrevem i(t) nos quatro i n t e r v a l o st,0 ,0 ≤t-25m s ,25m s ≤t ≤50m set.5

Use valores realistas de indutor do Apêndice H para construir combinações em série e em paralelo de indutores para obter as indutâncias equivalentes especificadas a seguir. Tente minimizar o número de

Inicialmente, não havia nenhuma energia armazenada no indutor de 5 H do circuitoda Figura P6.12, quando ele foi ligado aos terminais do voltímetro. Em t = 0, a chave doindutor passou instantaneamente

Suponha que a energia inicial armazenada nos indutores da Figura P6.22 (a) e (b) seja igual a zero. Determine a indutância equivalente em relação aos terminais a,b.