Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 7.Problemas - Ex. 72
Determine no circuito com AOP da Figura 7.137. Parta do pressuposto de que v(0) = −2 V, R = 10 k e C = 10 F.
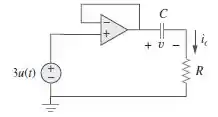
Passo 1
Para resolver este circuito, vamos ter que simplificá-lo, lembre-se que tanto o potencial no lado positivo é igual ao do lado negativo. Consequentemente, obtemos que
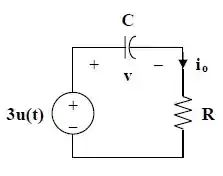
Com isso, se acharmos o potencial v(t), achamos a corrente .
Passo 2
Agora que já sabemos o circuito equivalente, podemos calcular v(t) do jeito que aprendemos. Assim a constante de tempo é:
Note que,
Substituindo na eq.
Obtemos
Passo 3
Como já sabemos a tensão nos terminais do capacitor, portanto,