Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 8.Questões para revisão - Ex. 9
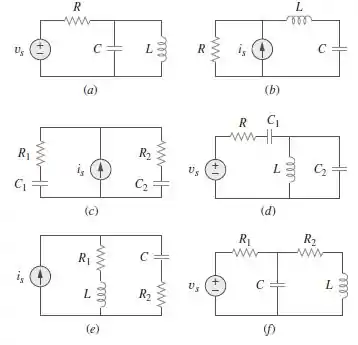
Associe os circuitos da Figura 8.61 aos itens a seguir:
(i) circuito de primeira ordem
(ii) circuito de segunda ordem em série
(iii) circuito de segunda ordem em paralelo
(iv) nenhuma das alternativas anteriores
Passo 1
Sabemos que, um circuito de primeira ordem, ele é composto por RC ou RL. Desse modo o item que condiz com essa afirmação é o item c). Logo
(i)-c
Um circuito de segunda ordem em série é um circuito RLC em que pelo menos LC estão em série. Desse modo o item que condiz com essa afirmação é o item b). Preste atenção para item e), se fizermos a transformação de fonte de corrente para a fonte de tensão, RLC vão estar em paralelo, logo,
(ii)-b,e
Um circuito de segunda ordem em paralelo é um circuito RLC em que pelo menos LC estão em paralelo. Desse modo o item que condiz com essa afirmação é o item a). Logo
(iii)-a
Portanto os circuitos restantes são condizem com nenhuma das alternativas anteriores,
(iv)-d,f
Resposta
(i)-c; (ii)-b,e; (iii)-a; (iv)-d,f