Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 13.Problemas - Ex. 12
Determine a indutância equivalente, , no circuito da Figura 13.81.
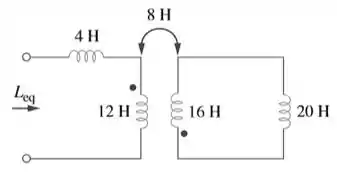
Passo 1
Essa questão exige um pouquinho de atenção a mais, mas não se procupem! Primeiramente temos que nos atentar para a posição dos enrolamentos nas bobinas. Notem que eles estão invertidos na indutancia mutua! Considerando , temos:
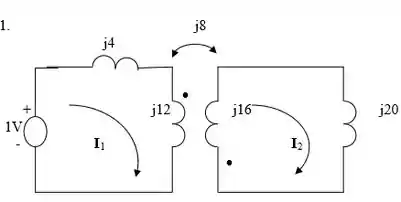
Passo 2
Para esse circuito, podemos aplicar uma LKT rapidinha, para obter:
Resolvendo esse sistema, temos que , portanto:
Podemos também usar um equivalente T para o transformador e achar a indutância equivalente!
Resposta
Exercícios de Livros Relacionados
As autoindutâncias de dois enrolamentos acoplados magneticamente são L 1 = 180μ HeL 2 = 500μ H . O meio de acoplamento é não magnético. Se o enrolamento 1 tiver 300 espirais e o enrolamento 2,500 espi
Dois enrolamentos acoplados magneticamente são enrolados em um núcleo não magnético.A autoindutância do enrolamento 1 é 288 mH, a indutância mútua é 90 mH, o coeficiente de acoplamento é 0,75 e a estr