Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 13.Problemas - Ex. 11
Use a análise de malhas para determinar na Figura 13.80, onde
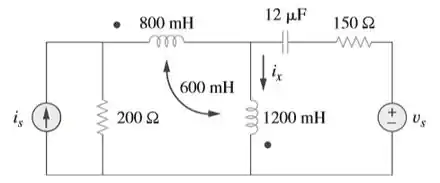
Passo 1
Okaaay galerinha, juntos mais uma vez! Essa questão é tranquila gente, vamos mastigar ela com calma e vai dar tudo certo! O segredo dessa questão está na gente fazer as malhas certinhas que o resto sai no automatico! Primeiro vamos transformar os capacitores e indutores em impedancias complexas!
Depois de transformar a fonte de conrrente em uma fonte de tensão, temos o circuito abaixo!
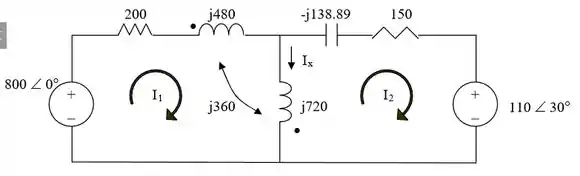
Passo 2
Fazendo uma rapidinha analise das malhas, temo que para a malha 1:
Para a malha 2,
Na forma de matrizes:
Passo 3
Essa matriz é um tanto quanto punk, então vamos resolver usando MATLAB! Teremos que:
Portanto,
Resposta
Exercícios de Livros Relacionados
Obtenha o equivalente de Norton nos terminais a-b do circuito da Figura 13.85
No circuito da figura abaixo, Z L é um indutor de 15m H com impedância de j 40Ω . Determine Z e n t quando k = 0,6 .
Determine o equivalente de Thévenin à esquerda da carga Z no circuito da figura abaixo.
Determine uma seção T equivalente que possa ser usada para substituir o transformador na Figura abaixo.
O coeficiente de acoplamento do Problema 6.47 é aumentado para 1,0.Se i 1 for igual a 6 A, qual será o valor de i 2 que resultará em energia armazenada nula?Há qualquer valor fisicamente viável de i 2