Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 17.Problemas - Ex. 54

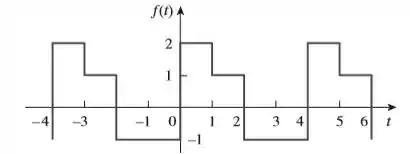
Determine a série de Fourier exponencial para a função da figura.

Passo 1

De acordo com o nosso amigo Fourier exponencial, podemos obter c n (coeficientes da série de Fourier) através da integral:

c n = 1 T ∫ - T / 2 T / 2 f t e - j ω 0 n t   d t

No nosso caso, temos uma função de período T = 4 , ou seja...

ω 0 = 2 π 4 = π 2

Substituindo então no c n ...

c n = 1 4 ∫ 0 4 f t e - j n π 2 t d t   →

Como a nossa função tem definições diferentes...

c n = 1 4 ∫ 0 1 2 e - j n π 2 t d t + ∫ 1 2 1 e - j n π 2 t d t + ∫ 2 4 - 1 e - j n π 2 t d t   →

c n = 1 4 2 ∫ 0 1 e - j n π 2 t d t + ∫ 1 2 e - j n π 2 t d t - ∫ 2 4 e - j n π 2 t d t   →

Podemos calcular essa integral! Bora?

Passo 2

Como a integral de...

∫     e - a t d t = - e - a t a

Então...

c n = 1 4 2 - e - j n π 2 t j n π 2 0 1 + - e - j n π 2 t j n π 2 1 2 - - e - j n π 2 t j n π 2 2 4   →

c n = j 2 n π 2 e - j n π 2 t 0 1 + e - j n π 2 t 1 2 - e - j n π 2 t 2 4   →

c n = j 2 n π 2 e - j n π 2 - e 0 + e - j n π - e - j n π 2 - e - j 2 n π - e - j n π   →

Simplificando...

c n = j 2 n π 3 e - j n π 2 - 3 + 2 e - j n π  

Passo 3

Ta aí! Os nosso coeficientes. De acordo com Fourier podemos então representar f assim:

f t = ∑ n = 0 ∞ c n e j ω 0 n t =

∑ n = 0 ∞ j 2 n π 3 e - j n π 2 - 3 + 2 e - j n π e j ω 0 n t

Resposta

f t = ∑ n = 0 ∞ j 2 n π 3 e - j n π 2 - 3 + 2 e - j n π e j ω 0 n t

Ver Outros Exercícios desse livro