Enunciado
Elétrica - Sadiku - Fundamentos de Circuitos Elétricos- Ed: 5º - Capítulo 6.Problemas - Ex. 53
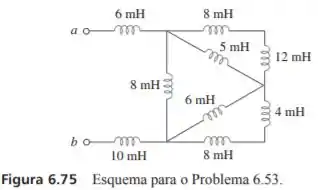
Determine a nos terminais do circuito da figura 6.75.
Passo 1
Da forma como foi apresentado o circuito fica muito complicado de enxergar quais resistores estão em paralelo e quais estão em série. Sendo assim, para facilitar nossa vida vamos sinalizar nossos nós para reescrevermos nosso circuito de uma forma mais simples e facilitar nossas contas. Então,
Agora que nomeamos os nós podemos redesenhar nosso circuito de uma maneira bem mais simples da seguinte forma
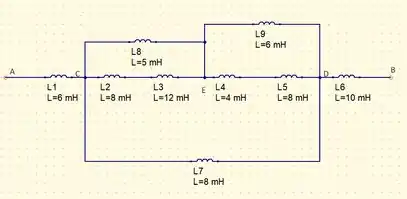
Devemos lembrar ainda que a regra que vale para os indutores é igual a regra que vale para os resistores ou seja
Onde representa uma associação em série e associação em paralelo.
Passo 2
Sendo assim, podemos fazer as associações em série dos indutores além do obtendo o circuito simplificado
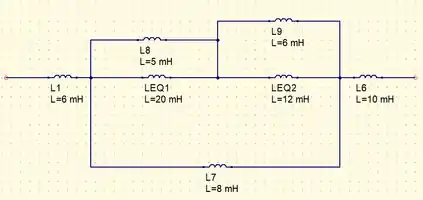
Associando , juntamente com os indutores e vamos ter um circuito mais simples ainda dado por
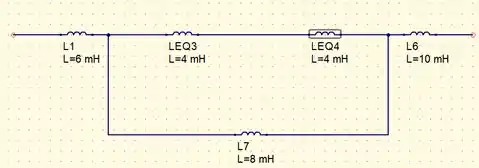
Associemos agora os indutores que estão em série e vamos obter
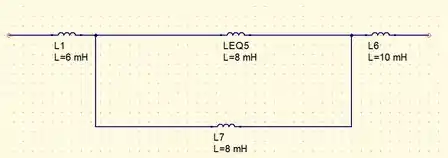
Fazendo associados em paralelo vamos obter o circuito mais simplificado dado por
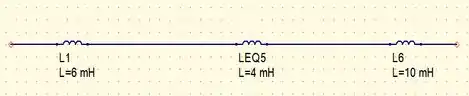
Por fim, para finalizar nosso problema basta somarmos todas as indutâncias e vamos obter